Uygulama 1: Döngüler ve Kararlar

Döngüler ve Kararlar Uygulama

• n bilinmeyenli n doğrusal denklemin çözümü

• En küçük kareler yöntemi

Dr. Emre S. Taşcı, emre.tasci@hacettepe.edu.tr
Fizik Mühendisliği Bölümü
Hacettepe Üniversitesi

Doğrusal denklem setleri

Mühendislerin işleri, mevcut sorunlara çözüm getirmektir. Gerçek hayattaki bu sorunları da denklemler olarak temsil eder, onları -mümkünse analitik, değilse veya çok zorluysa sayısal olarak- çözmeye uğraşırız.

Bu dersimizde, bilinmeyenlerin en büyük kuvvetinin 1 olduğu denklem setlerini ele alacağız, bu tür denklemlere doğrusal denklem diyoruz (bir doğrunun denklemini tanımladıkları için). Örneğin: \(y=m x + n\) denklemi, parametreleri olan \(x\)’in de, \(y\)’nin de kuvvetinin 1 olmasından ötürü eğimi \(m\) olup, y eksenini \(n\) değerinde kesen bir doğruyu verir.

\(y = mx+n\) denkleminde, 2 bilinmeyen var \((x,y)\). 2 bilinmeyene 1

Elimizde her 2 bilinmeyenli 2 denklem bulduğumuzda doğal olarak grafik çizip, kesiştikleri noktaları saptayamayacağımızdan ötürü, biraz daha sistematik olmak durumundayız. Genelleştirmek gerekirse, m bilinmeyenli n doğrusal denklem takımından bahsetmekteyiz. Bu denklem takımları m ve n’in birbirlerine olan büyük, küçük, eşit durumlarına göre üçe ayrılır:

1. Yetersiz Tanımlı Doğrusal Takım (\(m>n\)): Bilinmeyen sayısı m’in, denklem sayısından fazla olması durumunda, denklem takımını sağlayan sonsuz tane çözüm olur.

2. Bağımsız Doğrusal Takım (\(m = n\)): Bilinmeyen sayısı denklem sayısına eşitse, her bir bilinmeyenin bütün denklemleri sağlayan sadece bir adet değeri olacaktır.

3. Aşırı Tanımlı Doğrusal Takım (\(m < n\)): Denklem sayısının bilinmeyen sayısından fazla olması durumunda ortaya çıkan bu takımda, çözüm olmasa da, gerçek hayatta genel olarak bu türden denklem takımları ile ilgilendiğimizden, elimizdeki denklemleri mümkün mertebe sağlayan değerleri bulmaya çalışırız. Bu tür denklem takımlarına örnek olarak çeşitli kütleleri (\({m_i}\)) bir tartıya koyup, ağırlıklarını (\({F_i}\)) ölçtüğümüz bir deney yaptığımızı düşünelim: gerek ortamdan, gerekse tartıdaki hassasiyet ve hatalardan dolayı hiçbir zaman tam olarak:

\[F_i = m_i g\]

bulamayız, onun yerine mesela şöyle bir veri setimiz olabilir:

\(m_i\) (kg)	\(F\) (N)
1.0000	9.8818
2.0000	18.9612
3.0000	29.5044
4.0000	36.7874
5.0000	53.2063

Teoride \(F = m\cdot g\) olduğunu biliyoruz ama pratikte bu pek doğrulanmıyor. Elimizde 1 bilinmeyen (g) var ama 5 tane denklem var. Grafiğini çizdirirsek:

import numpy as np
import matplotlib.pyplot as plt

m = np.arange(1,6)
F = np.array([9.8818, 18.9612, 29.5044, 36.7874, 53.2063])

plt.plot(m,F,"s")
plt.show()

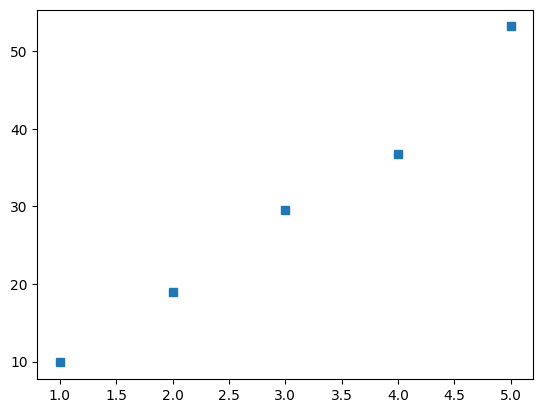
Denklemimiz doğrusal olduğundan lineer bir ilişki olduğunu biliyoruz ama işte o doğruyu bütün bu noktalardan geçirmeyeceğimiz de apaçık. O zaman hepsinin mümkün mertebe en yakınından geçen doğruyu alacağız, onu da “en küçük kareler yöntemi” denilen yöntemle elde edeceğiz.

İlk olarak bilinmeyen sayısının bağımsız denklem sayısına eşit olduğu “Bağımsız Doğrusal Denklem Takımları” ile ilgileneceğiz (n bilinmeyenli n doğrusal denklem). Çok temel olduğu için onlarca çözüm yöntemi var, biz bu yöntemlerden Gauss eleme yöntemini ele alacağız.

n bilinmeyenli n doğrusal denklemin Gauss Eleme Yöntemi ile çözümü

İki bilinmeyenli iki denklem sistemi

Özel Çözüm (Örnek)

Elimizde

\[\begin{split}5y = 2x+8\\4y=3x + 5\end{split}\]

şeklinde iki bilinmeyenli, iki denklemimiz olsun. Bu denklemleri düzenleyip:

\[\begin{split}\begin{align}(1):\;2x - 5y &= -8\\(2):\;-3x+4y&=5\end{align}\end{split}\]

olarak yazalım. Denklemlerin solunu da, sağını da aynı sayıyla çarparsak/bölersek, aynı sayıyı eklersek/çıkarırsak, kısacası iki tarafa da aynı matematiksel işlemi uygularsak eşitlik bozulmaz. O halde biz de 1. denklemi önce 2’ye bölelim (böylelikle x’in katsayısı 1 olur); ardından (2. denkleme doğrudan eklediğimizde ondaki “-3x”ü götürmesi için) -3 ile çarpıp 2. denklemden çıkaralım:

\[\begin{split}\begin{align}\frac{-3}{2}\times(1)&:\;\frac{-3}{2}\left[2x - 5y = -8 \right]\rightarrow -3x + \frac{15}{2}y = 12\\ (2)-\left[\frac{-3}{2}\times(1)\right]&:\left[-3x+4y=5\right]-\;\left[-3x + \frac{15}{2}y = 12\right] \\&=\left(-3+3\right)x +\left(4- \frac{15}{2}\right)y = \left(5-12\right)\\&\frac{-7}{2}y=-7\\&\Rightarrow y = 2\end{align}\end{split}\]

artık y değerine bildiğimize göre, iki denklemden birine bunu koyup, x’i bulabiliriz. 1. denklemi kullanalım:

\[2x-5\cdot(2) = -8\rightarrow x=\frac{-8+10}{2} = 1\]

Demek ki çözüm setimiz: \((x,y) = (1,2)\) imiş.

Genel Çözüm

Elimizde:

\[\begin{split}(1):\;a_{11} x + a_{12} y = b_1 \\(2):\;a_{21} x + a_{22} y = b_2\end{split}\]

şeklinde iki bilinmeyenli, iki denklemimiz olsun (\(a\)’lar ve \(b\)’ler verilmiş durumda, biz \(x\) ve \(y\)yi bulmaya çalışıyoruz). Her seferinde ayrı ayrı \(x\)’i ve \(y\)’yi yazmamak için katsayılarını matrise tanımlayıp oradan devam edelim (\(b\)’leri de matrise katarsak şöyle bir durum oluyor):

\[\begin{split}a_{11} x + a_{12} y = b_1 \\a_{21} x + a_{22} y = b_2\\\Rightarrow \begin{bmatrix}a_{11}&a_{12}&\|& b_1\\a_{21}&a_{22}&\|& b_2\end{bmatrix}\end{split}\]

Denklemlerin ikisi de (adı üstünde) eşitlik olduğundan iki taraftan aynı sayıyla çarptığımız zaman hala sol taraf sağ tarafa eşit olacaktır. Biz de 1. denklemi \(\frac{a_{21}}{a_{11}}\) ile çarpıp, 2. denklemden çıkarmak suretiyle, 2. denklemden x’i eleyelim:

\[\begin{split}\begin{bmatrix}a_{11}&a_{12}&\|& b_1\\0&a_{22}-\left(\frac{a_{21}}{a_{11}}a_{12}\right)&\|& b_2-\left(\frac{a_{21}}{a_{11}}b_{1}\right)\end{bmatrix}\end{split}\]

Bu işlemden sonra 2. denklemde sadece \(y\) kaldı, onu da yalnız bırakırsak (yani 2. denklemi \(y\)’nin katsayısı olan \(a_{22}-\left(\frac{a_{21}}{a_{11}}a_{12}\right)\) değerine bölersek:

\[ y=\frac{b_2-\left(\frac{a_{21}}{a_{11}}b_{1}\right)}{a_{22}-\left(\frac{a_{21}}{a_{11}}a_{12}\right)}\]

olarak bulunur. \(y\)’nin bu değerini 1. denkleme koyduğumuzda ise (yani 1. denklemde \(y\) gördüğümüz yere \(\frac{b_2-\left(\frac{a_{21}}{a_{11}}b_{1}\right)}{a_{22}-\left(\frac{a_{21}}{a_{11}}a_{12}\right)}\) yazarak) \(x\)’i de buluruz:

\[a_{11}x + a_{12}y = b_1 \rightarrow x = \frac{b_1 - a_{12}y}{a_{11}}\]

\[y=\frac{b_2-\left(\frac{a_{21}}{a_{11}}b_{1}\right)}{a_{22}-\left(\frac{a_{21}}{a_{11}}a_{12}\right)}\Rightarrow x=\frac{b_1 -a_{12}{\frac{\left(-\frac{a_{21}}{a_{11}}b_{1}\right)+b_2}{\left(-\frac{a_{21}}{a_{11}}a_{12}\right)+a_{22}}}}{a_{11}}\]

Bulduklarımızı bu kısmın başındaki özel örneğimize uygulayalım:

\begin{align}2x - 5y &= -8-3x+4y&=5\end{align}

Matrise çevirip, numpy’dan devam edelim:

# Matrisleri tanımlarken ilk elemanı noktalı (ondalıklı)
# şekilde yazıyoruz ki, numpy onları tamsayılar matrisi
# olarak değil de, ondalıklı sayılar (float) matrisi olarak
# ele alsın (yoksa işlem sonuçarı da tamsayılara yuvarlanır)

A = np.array([[2.,-5],[-3,4]])
b = np.array([[-8.,5]]).T
print(A)
print(b)

[[ 2. -5.]
 [-3.  4.]]
[[-8.]
 [ 5.]]

# Satır çok uzun olduğu için işlemi "\" kesme işareti
# ile ikiye ayırdık. Ayrıca, python'da indisler 0'dan
# başladığından, formüldeki indislerden 1 düşük yazdık
# (örn. A_21 -> A[1,0] olarak temsil edildi)

y = (b[1] - (A[1,0]/A[0,0]*b[0])) \
  / (A[1,1]-(A[1,0]/A[0,0]*A[0,1]))
y

array([2.])

x = (b[0] - A[0,1]*y) / A[0,0]
x

array([1.])

Bu işlemleri (elimizde sayılarla tanımlanmış bir matris olduğundan) doğrudan matris üzerinden de yapabilirdik:

Önce A ile b’yi birleştirip, M matrisini oluşturalım:

M = np.concatenate((A,b),axis=1)
M

array([[ 2., -5., -8.],
       [-3.,  4.,  5.]])

1. satırı (M[0,:]), ilk katsayısına (M[0,0] = 2) bölüp, 2.nin ilk katsayısıyla (M[1,0]=-3) çarpıp, 2. satırdan (M[1,:]) çıkaralım:

M[1,:] = M[1,:] - (M[0,:]/M[0,0] * M[1,0])
M

array([[ 2. , -5. , -8. ],
       [ 0. , -3.5, -7. ]])

2. denklemde (satırda) \(y\) yalnız kaldığına göre, son elemanı (M[1,-1] = -7), 2. elemana (M[1,1] = -3) bölerek onu bulabiliriz:

y = M[1,-1] / M[1,1]
y

2.0

\(x\)’i bulmak için de bulduğumuz bu \(y\) değerini kullanacağız. İlk satırda (denklemde) (M[0,:]) son elemandan (M[0,-1] = -8) \(y\)’nin katsayısı (M[0,1] = -5) ile \(y\)’nin değerinin çarpımını çıkarıp, \(x\)’in katsayısına (M[0,0] = 2) böleceğiz. Böyle yazınca çok karmaşık geliyor ama aslında dediğimiz şey: elimizde \(ax + by = c\) gibi bir denklem varsa, \(y\)’nin değerini de biliyorsak, \(x = \frac{c - by}{a}\) olacağı! 8)

x = (M[0,-1] - M[0,1] * y) / M[0,0]
x

1.0

Üç bilinmeyenli üç denklem sistemi

(Bağımsız) Denklem sayımız üç olduğunda onu da:

\[\begin{split}a_{11} x + a_{12} y + a_{13} z= b_1 \\a_{21} x + a_{22} y + a_{23} z= b_2\\a_{31} x + a_{32} y + a_{33} z= b_3\\\Rightarrow \begin{bmatrix}a_{11}&a_{12}&a_{13}&\|& b_1\\a_{21}&a_{22}&a_{23}&\|& b_2\\a_{31}&a_{32}&a_{33}&\|& b_3\end{bmatrix}\end{split}\]

olarak düşünüp, önce 1. denklemi kullanıp, 2. ve 3. denklemlerdeki \(x\) katsayılarını eleyelim. Bunun için 1. denklemi \(\frac{a_{21}}{a_{11}}\) ile çarpıp 2.’den; \(\frac{a_{31}}{a_{11}}\) ile de çarpıp, 3. denklemden çıkartırız.

Sonrasında sıra 3. denklemdeki \(y\) katsayısını elemeye gelir. 1. denklemde herhangi bir işlem yapıp 3. denklemde çıkarmamız halinde \(x\)’in de geri geleceğinden ötürü, 3. denklemdeki \(y\) katsayısını 2. denklemi kullanarak eleriz. 2. denklemi kendisinin o aşamadaki \(y\) katsayısına bölüp, 3. denklemin o aşamadaki \(y\) katsayısı ile çarpıp, 3. denklemden ekleriz. (Formüler olarak çok karışık ve korkutucu bir hal aldığından, somut bir örnek üzerinden gidelim):

Denklemlerimiz:

\[\begin{split}\begin{align}2x-5y+3z&=7\\x+3y-4z&=-2\\-2x+2y-3z&=-10\end{align}\end{split}\]

olsunlar. Bunları numpy’a girelim:

A = np.array([[2., -5, 3],[1, 3, -4],[-2, 2, -3]])
b = np.array([[7, -2, -10]]).T
M = np.concatenate((A,b),axis=1)

print("A:\n",A)
print("b:\n",b)
print("M:\n",M)

A:
 [[ 2. -5.  3.]
 [ 1.  3. -4.]
 [-2.  2. -3.]]
b:
 [[  7]
 [ -2]
 [-10]]
M:
 [[  2.  -5.   3.   7.]
 [  1.   3.  -4.  -2.]
 [ -2.   2.  -3. -10.]]

2. satırdaki \(x\) katsayısını elemek için 1. satırı 1. satırın \(x\) katsayısına (2) bölüp, ikinci satırın \(x\) katsayısı (1) ile çarpıp, 2. satırdan çıkartırız:

M[1,:] = M[1,:] - (M[0,:] / M[0,0] * M[1,0])
M

array([[  2. ,  -5. ,   3. ,   7. ],
       [  0. ,   5.5,  -5.5,  -5.5],
       [ -2. ,   2. ,  -3. , -10. ]])

3. satırdaki \(x\) katsayısını götürmek içinse 1. satırı 1. satırın \(x\) katsayısına (2) bölüp, üçüncü satırın \(x\) katsayısı (-2) ile çarpıp 3.’den çıkartırız:

M[2,:] = M[2,:] - (M[0,:] / M[0,0] * M[2,0])
M

array([[ 2. , -5. ,  3. ,  7. ],
       [ 0. ,  5.5, -5.5, -5.5],
       [ 0. , -3. ,  0. , -3. ]])

Şimdi sırada 2. satırı kullanarak, 3. satırın \(y\) katsayısını elemek var. Bunun için de, 2. satırı 2. satırın \(y\) katsayısına (5.5) bölüp, 3. satırın \(y\) katsayısı (-3) ile çarparak 3. satırdan çıkartırız:

M[2,:] = M[2,:] - (M[1,:] / M[1,1] * M[2,1])
M

array([[ 2. , -5. ,  3. ,  7. ],
       [ 0. ,  5.5, -5.5, -5.5],
       [ 0. ,  0. , -3. , -6. ]])

Buradan (3. satırdan) doğrudan \(z = \frac{-6}{-3} = 2\) olduğunu görüyoruz.

Bunu 2. satırda kullanırsak: \(y = \frac{-5.5 + 5.5z}{5.5} = \frac{-5.5 + 5.5\times2}{5.5}=\frac{5.5}{5.5}= 1\)

Artık \(z\) de, \(y\) de elimizde olduğuna göre, \(x\)’i de bulabiliriz:

\(x = \frac{7-3z+5y}{2} = \frac{7-3\times2+5\times1}{2} = \frac{6}{2} = 3\)

Genele sistematik uygulama

n bilinmeyenli n denklemimizde bilinmeyenlerin katsayılarını \(A\) matrisinde, eşitliklerini de \(b\) sütun vektöründe toplayalım. Sonra da bunları yukarıda yaptığımız gibi birleştirip \(n\times (n+1)\)’lik bir \(M\) matrisinde toplayalım.

İleriye eleme aşaması

İlk yapmamız gereken 1. satırı, 1. satırın 1. sütununa bölüp, altındaki her bir satırın 1. sütununun değeriyle çarpıp o satırdan çıkararak o satırlardaki ilk terimi elemek. Bu işlem bitince, bu sefer 2. satırı, 2. satırın 2. sütununa bölüp, altındaki her bir satırın 2. sütununun değeriyle çarpıp o satırdan çıkararak, o satırlardaki ikinci terimi elemek; sonra 3. satıra geçip, onu 3. satırın 3. sütununa bölüp, altındaki her bir satırın 3. sütununun değeriyle çarpıp o satırdan çıkararak 3. terimleri elemek, …

Örüntüyü (“pattern”i) fark edebildiniz mi? (Eğer edemediyseniz, bir de sesli okuyun, örüntü de, kafiyeli bir şiir gibi dilinize gelecektir ;)

sanki-kod’da (“pseudo-code”) bunu şu şekilde belirtebiliriz:

for eleyen_satir = 0:n-1 for etkilenen_satir = eleyen_satir+1:n etkilenen_satir = etkilenen_satir - (eleyen_satir)/(eleyen_satir’in eleyen_satir’inci sutununun degeri) * (etkilenen_satir’in eleyen_satir’inci sutununun degeri ile carpilmis hali)

Yukarıda çözdüğümüz örnekte bir uygulamayı deneyelim bakalım:

A = np.array([[2., -5, 3],[1, 3, -4],[-2, 2, -3]])
b = np.array([[7, -2, -10]]).T
M = np.concatenate((A,b),axis=1)

n = M.shape[0] # satır (denklem) sayısı

print("{:d}x{:d}'lik bir denklem takımı çözüyoruz!\n".format(n,n))

# İleriye eleme aşaması:
for eleyen_satir_no in range(n-1):
    for etkilenen_satir_no in range(eleyen_satir_no+1,n):
        M[etkilenen_satir_no,:] = M[etkilenen_satir_no,:] \
          - (M[eleyen_satir_no,:] / M[eleyen_satir_no,eleyen_satir_no]\
             * M[etkilenen_satir_no,eleyen_satir_no])

print("İleriye eleme aşamasının sonucu:")
print(M)

3x3'lik bir denklem takımı çözüyoruz!

İleriye eleme aşamasının sonucu:
[[ 2.  -5.   3.   7. ]
 [ 0.   5.5 -5.5 -5.5]
 [ 0.   0.  -3.  -6. ]]

Geriye yerine yerleştirme aşaması

İlk (0.) satırdan (denklemden) başlayıp, eleye eleye sona (n-1. satıra/denkleme geldik. Bu satırda yapılacak tek şey, son (n.) sütundaki denklem eşitliğini, sondan bir önceki (n-1.) değere (yani son bilinmeyenin katsayısına bölmek). Özel örneğimizde bu: \(z = \frac{-6}{-3}\) demeye karşılık geliyor. (Python’da indislerin 0’dan başlaması işleri biraz karıştırsa da aslında yaptığımız gayet basit ve dosdoğru).

Sondan bir önceki (Python’da n-2 indisli) satıra geldiğimizde, bu denklemin eşitliği son (n-1 indisli) sütunda, bir alttaki satırdan bulduğumuz bilinmeyenin katsayısı sondan bir önceki (n-2 indisli) sütunda, bu denklemdeki bilinmeyenin katsayısı da sondan iki önceki sütunda duruyor. Artık ondan sonraki değişken bilindiğinden, o bilinmeyeni yerine koyup, katsayısı ile çarpıp, eşitliğin değerinden çıkarıp, bu satırın bilinmeyeninin katsayısına bölersek, bu satırın bilinmeyenini de bulmuş oluruz.

Genel olarak yazarsak:

\(i\) indisli satıra geldiğimizde, o satırın bilinmeyeni \(i\) indisli sütunda olacak, kendisinden önceki sütunların katsayıları 0 olacak, kendisinden sonraki değişkenler de o aşamada bilinir olacağından, son sütundaki değerden alttaki satırlardan (denklemlerden) bulduğumuz değerleri yerine koyup katsayıları ile çarpımlarını çıkarırsak, ve son olarak da mevcut bilinmeyenin katsayısına bölersek işlem tamam olacaktır. Yine çok laf kalabalığı gayet dosdoğru ve basit bir matematiksel işlemi karmaşık gösterdi, o yüzden bir örnek ile ilerleyelim, elimizdeki \(i\) indisli satır şöyle olsun:

\[\begin{matrix}0&0&\dots&0&a_{i}&a_{i+1}&a_{i+2}&\dots&a_{n-1}&b_i\end{matrix}\]

\(a_i\) bizim mevcut bilinmeyenimizin katsayısı, ondan sonra gelen \(a_*\) katsayıları artık bilinen değişkenlerin katsayıları, en sondaki \(b_i\) de o denklemin sağ tarafındaki eşitlik. Bu da demek oluyor ki, bizim \(x_i\) bilinmeyenimizi, şu şekilde çekebiliriz:

\[\begin{split}\begin{gather*}a_i x_i + a_{i+1} x_{i+1} + \dots + a_{n-1} x_{n-1} = b_i\\ a_i x_i = b_i-\left(a_{i+1} x_{i+1} + \dots + a_{n-1} x_{n-1}\right)\\ \\ x_i = \frac{b_i-\left(a_{i+1} x_{i+1} + \dots + a_{n-1} x_{n-1}\right)}{a_i} \end{gather*}\end{split}\]

Üstteki denklemde, paydadaki parantez içindeki katsayılar ile ilgili değişkenlerinin çarpımına dikkat edersek, bunu aslında tüm katsayılar ile değişkenlerin çarpımı gibi yazabileceğimizi görebiliyoruz. Bunu, o satırın ilgili değişkeninden önceki bütün bilinmeyenlerin katsayılarının 0 olması sağlıyor; ufak bir fark, o satırın ilgili değişkeninin toplama girmiyor oluşu ki, bunu da küçük bir “hile” ile halledeceğiz.

Matematiksel olarak özetlersek: \(\vec{a}\), o satırın katsayılar vektörü olsun, \(\vec{x}\) de değişkenler vektörü. Eğer değişkenler vektörünün ilk \(i\) elemanını (yani bilmediğimiz değişkenlerin değerlerini) 0 olarak tanımlarsak \(\vec{a}.\vec{x}\) skaler çarpımı bize tam da istediğimiz toplamı verir \(\left(\vec a . \vec x = \sum_{i}{a_i.x_i}\right)\). Formül şeklinde yazarsak:

\[x_i = \frac{b_i - \vec {a} . \vec {x}}{a_i}\]

Gelelim “hilemize”: başlangıçta bilinmeyenlerin tutulduğu \(\vec x\) dizisinin bütün elemanlarını 0 yapıyor, değerleri buldukça ilgili bileşenleri güncelliyoruz. Böylelikle yukarıdaki skaler çarpımda bilinmeyenler o sırada 0 olduğundan toplama hiçbir katkıda bulunmuyorlar! 8)

M

array([[ 2. , -5. ,  3. ,  7. ],
       [ 0. ,  5.5, -5.5, -5.5],
       [ 0. ,  0. , -3. , -6. ]])

n = M.shape[0]

# Bilinmeyenlerimize başlangıçta 0 değeri verip,
# n boyutlu bir x vektöründe tutuyoruz
x = np.zeros(n)

for i in range(n-1,-1,-1):
    print("{:d} indisli satırı işliyoruz:".format(i))
    b_i = M[i,-1]
    a_i = M[i,i]
    a = M[i,:-1]
    ax = np.dot(a,x)
    x[i] = (b_i - ax ) / a_i
    print("\tBu denklemin bilinmeyeni: x[{:d}] = {:.3f}"\
          .format(i,x[i]))

print("\n")
print("Bilinmeyenler bulundu:",x)

    

2 indisli satırı işliyoruz:
	Bu denklemin bilinmeyeni: x[2] = 2.000
1 indisli satırı işliyoruz:
	Bu denklemin bilinmeyeni: x[1] = 1.000
0 indisli satırı işliyoruz:
	Bu denklemin bilinmeyeni: x[0] = 3.000


Bilinmeyenler bulundu: [3. 1. 2.]

Naif, temiz kalpli, saf Gauss eleme yöntemi

Bu notlarda kullandığımız eleme yönteminin tam ismi aynen bu: Naif Gauss Eleme Yöntemi (Naïve Gauss Elimination Method). Böyle naif denmesinin sebebi, birtakım tuzaklara karşı önhazırlıksız olmasından, verilen matrisin sıralanmasından kaynaklı olarak bazı işlemlerinin uzun ve kötü hassasiyetle çıkabiliyor oluşundan kaynaklanıyor. Daha optimize ve kurnaz hali Gauss-Jordan Eleme Yöntemi olarak anılıyor (çok da farklı, kompleks bir şey değil bu arada:, sadece orada satırların sırasını belli bir düzene göre değiştirip, öyle işleme alıyoruz).

“Bunu yapan komut var zaten”

Hesaplarımız sıklıkla “n bilinmeyenli n denklemin çözümü” problemine dönüştüğünden, bunu hızlıca yapan hazır bir komutumuz da mevcut. Ama öncesinde bir başka yaklaşımdan bahsedelim:

Denklemlerimiz:

\[\begin{split}\begin{align}2x-5y+3z&=7\\x+3y-4z&=-2\\-2x+2y-3z&=-10\end{align}\end{split}\]

olsun. Bu denklem setini, bir matrix ve vektörün çarpımı olarak şu şekilde yazabiliriz:

\[\begin{split}\begin{bmatrix}2&-5&3\\1&3&-4\\-2&2&-3\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}7\\-2\\-10\end{bmatrix}\end{split}\]

Katsayılar matrisine \(A\), bilinmeyenler vektörüne \(\vec x\), sonuçların olduğu vektöre de \(\vec b\) diyelim. Böylelikle elimizdeki işlem basit bir matris-vektör çarpım eşitliği olarak yazılabilir:

\[A\cdot \vec x = \vec b\]

Eşitliğin iki tarafını soldan \(A\) matrisinin tersi ile çarpacak olursak, tersiyle çarpım birim matrisi vereceğinden \(\vec x\) yalnız kalır:

\[\begin{split}\begin{align}\underbrace{A^{-1}A}_{\mathbb 1}\cdot \vec x &= A^{-1}\vec b\\ \rightarrow\vec x &= A^{-1}\vec b\end{align}\end{split}\]

Bunu python’da yaparsak:

A = np.array([[2., -5, 3],[1, 3, -4],[-2, 2, -3]])
b = np.array([[7, -2, -10]]).T
A,b

(array([[ 2., -5.,  3.],
        [ 1.,  3., -4.],
        [-2.,  2., -3.]]),
 array([[  7],
        [ -2],
        [-10]]))

x = np.dot(np.linalg.inv(A),b)
x

array([[3.],
       [1.],
       [2.]])

Tahmin edeceğiniz üzere, bu işlemin de hızlı çalışacak şekilde optimize edilmiş hazır bir fonksiyonu bulunmakta: np.linalg.solve(A,b):

np.linalg.solve(A,b)

array([[3.],
       [1.],
       [2.]])

Elimizde gerçekte kaç adet denklem var?

Bazen, elimizde n adet bağımsız denklem olduğunu sanarken, aslında bunların bazıları diğerlerinin lineer bileşimlerinden elde edilebilir, bu da doğal olarak yeni bir bilgi getirmediğinden, denklemleri çözmemiz mümkün olmaz. Örnek olarak aşağıdaki üç bilinmeyenli üç denklemi ele alalım:

\[\begin{split}\begin{align}6x+3y-z &= 18\\ 6x+y+2z&=45\\ 18x+13y-9z&=0\end{align}\end{split}\]

Denklemler ilk bakışta birbirlerinden epey alakasız görünseler de, dikkat edince 3. denklemin, 1. denklemin 5 katından, 2. denklemin 2 katının çıkarılmasıyla elde edilebileceği ortaya çıkar:

M = np.array([[6,3,-1],[6,1,2],[18,13,-9]])
M

array([[ 6,  3, -1],
       [ 6,  1,  2],
       [18, 13, -9]])

M[0,:]*5 - M[1,:]*2

array([18, 13, -9])

Bu da doğal olarak katsayılar matrisinin determinantının 0 olup, matrisin tersinin bulunmayacağı anlamına gelir.

np.linalg.det(M) # katsayılar 3x3'lük kısımda,
                 # son sütun denklem değerleri
                 # olduğundan onu ayırdık.

-3.330669073875456e-15

Verilen bir denklem setinin kaç adet bağımsız denklem içerdiğini o matrisin rütbesini (rank) sorarak öğrenebiliriz:

np.linalg.matrix_rank(M)

2

En küçük kareler yöntemi

Dersimizin başında, her zaman için elimizdeki bağımsız denklem sayısının bilinmeyen sayısına eşit olmayacağını, bazen denklem sayısının değişken sayısından daha fazla olduğu “Aşırı tanımlı doğrusal takım”dan bahsedip, yerçekimi ivmesini hesaplamak üzere tasarlanan bir deneyin ölçümlerini vermiştik.

\[F_i = m_i g\]

için yapılan ölçüm sonuçları şunlar olsun:

\(m_i\) (kg)	\(F\) (N)
1.0000	9.8818
2.0000	18.9612
3.0000	29.5044
4.0000	36.7874
5.0000	53.2063

import numpy as np
import matplotlib.pyplot as plt

m = np.arange(1,6)
F = np.array([9.8818, 18.9612, 29.5044, 36.7874, 53.2063])

plt.plot(m,F,"s")
plt.show()

Grafiğini çizdiğimizde, eğimin bize g’yi vereceği açık ama hangi doğrunun grafiğini almalıyız? Ya da bir başka deyişle, “en doğru doğru”yu nasıl tanımlarız? Akla ilk gelen, tabii ki bütün noktaların mümkün mertebe en yakınından geçen doğruyu almak. Peki o doğrunun denklemini nasıl elde ederiz? Bu soruya en iyi cevabı “En Küçük Kareler Yöntemi” vermekte.

Bu yöntemde elimizde bir \(y=mx+n\) doğrusunun olduğu varsayımıyla başlarız. Bu doğrunun elimizdeki \(x\) değerlerine karşılık gelen değerlerinin (bu değerleri “\(t\)” ile gösterelim) deneyde bulduğumuz \(y\) değerleri arasındaki mesafeleri hesaplayıp, bu mesafeleri mümkün oldukça küçük yapacak \(m\) ve \(n\) değerlerini bulmaya çalışırız.

Verileri elde ettiğimiz deney şöyle bir düzenek olabilir: elimizde 1 kg’dan 6 kg’a kadar 6 kütle var, bunları basküle koyup, ağırlıklarını Newton cinsinden ölçüyoruz.

Genelleştirme adına kontrol parametremiz olan kütleleri \(x\) ile, okuduğumuz ölçümler olan ağırlıkarı da \(y\) ile temsil edelim:

x = np.arange(1.,6)
y = np.array([9.8818, 18.9612, 29.5044, 36.7874, 53.2063])

Python’da doğrudan sembolik hesap yapılmadığından (yani “m” ve “n” olarak bilinmeyenleri denklemlere sokamayacağımızdan), işlemlerimizi “kağıt” üzerinde açalım:

Elimizde 5 adet veri ikilisi var. Bu ikililerin her birini x(i) ve y(i) ile gösterelim.

Örneğin:

x[4] = 5.0
y[4] = 53.2063

Doğrunun denkleminde x[i]ye karşılık gelen değeri t[i] ile gösterecek olursak, \(t_i = mx_i+n\) olur (örneğin, t[4] = m*[5.0] + n).

Doğru denkleminden bulduğumuz değer ile deneyde bulduğumuz değer arasındaki mesafe:

\[\begin{equation*} \mid{t_i - y_i}\mid = \sqrt{{(t_i - y_i)}^2} \end{equation*}\]

olarak tanımlanır. Biz bu değerin kendisinden çok, bu değeri minimum yapmakla, yani doğruyu noktaya mümkün olduğunca yakın geçirmekle ilgilendiğimizden dolayı hem işlemden tasarruf sağlamak (karenin kökü yerine sadece kare alma işlemi), hem de minimize ederken türev almak gerekliliğinden dolayı (mutlak değer fonksiyonunun 0 noktasında türevi tanımlı değildir) aralarındaki mesafenin karesini minimize edeceğiz (mesafenin karesi minimize olduğunda, mesafenin kendisi de minimize olmuş olur ne de olsa).

Bu durumda, doğrunun üzerindeki nokta ile deneyde okunan değerin aralarındaki farkın karesine “s” diyelim:

\[\begin{equation*} s_i = (y_i - (m x_i + n))^2 \end{equation*}\]

ve parentezi açınca da:

\[\begin{split}\begin{align} s_i &= (y_i - (m x_i + n))^2 = y_i^2 - 2 y_i(mx_i+n) + (mx_i+n)^2\\ s_i &= y_i^2 - 2m x_i y_i -2n y_i +m^2 x_i^2 +2 m n x_i + n^2 \end{align}\end{split}\]

Toplam hata her bir veri çiftinden gelen hataların (farkların) toplamına eşit olacak \(\left(S = \sum_{i=1}^N s_i\right)\).

Toplam hatayı denklem cinsinden yazacak olursak:

\[\begin{align} S = \sum_{i=1}^N s_i = \sum_{i=1}^N (y_i^2 - 2m x_i y_i -2n y_i +m^2 x_i^2 +2 m n x_i + n^2) \end{align}\]

Toplam hatanın iki tane parametresi (ve bizim için bilinmeyeni) var: m & n. Denklemi minimize edecek m & n değerlerini bulabilmek için her birine göre türev alıp, sıfıra eşitleriz:

\[\begin{split}\begin{align} \frac{\partial S}{\partial m} &= \sum_{i=1}^N \frac{\partial s_i}{\partial m} = \sum_{i=1}^N (-2 x_i y_i + 2 m x_i^2 + 2 n x_i) = 0\\ \frac{\partial S}{\partial n} &= \sum_{i=1}^N \frac{\partial s_i}{\partial n} = \sum_{i=1}^N (-2 y_i + 2 m x_i + 2 n) = 0 \end{align}\end{split}\]

işimiz bitmedi ama az kaldı… 8)

Elimizde iki adet, iki bilinmeyenli eşitlik var (hataların m ve n’ye göre türevleri ve onların sıfıra eşit oluşları). Denklemleri m ve n’nin çarpanları olacak şekilde düzenlersek:

\[\begin{split}\begin{align} \left(\sum_{i=1}^N 2x_i^2\right)m + \left(\sum_{i=1}^N 2x_i\right)n &= \left(\sum_{i=1}^N 2x_i y_i\right)\\ \left(\sum_{i=1}^N 2x_i\right)m + \left(\sum_{i=1}^N 2\right)n &= \left(\sum_{i=1}^N 2 y_i\right) \end{align}\end{split}\]

Parantez içindeki bütün terimleri x[i] ve y[i]leri bildiğimizden dolayı döngü üzerinden hesaplatabiliriz.

Kolay anlaşılması açısından:

\[\begin{split}\begin{gather*} A_{11} = \sum_{i=1}^N 2x_i^2 ,\quad A_{12} = A_{21} = \sum_{i=1}^N 2x_i,\quad A_{22} = \sum_{i=1}^N 2\\ B_{11} = \sum_{i=1}^N 2x_i y_i,\quad B_{12} = \sum_{i=1}^N 2 y_i \end{gather*}\end{split}\]

dersek, denklemlerimiz:

\[\begin{split}\begin{equation*} A_{11}m + A_{12}n = B_{11}\\ A_{12}m + A_{22}n = B_{12} \end{equation*}\end{split}\]

halini alırlar. İkinci denklemde n’yi m cinsinden yazarsak:

\[\begin{equation*} n = \frac{B_{12} - A_{12}m }{A_{22}} \end{equation*}\]

bulunur; bunu da götürüp birinci denklemde n gördüğümüz yere yazdığımızda m’yi:

\[\begin{split}\begin{gather*} A_{11}m + A_{12} \left(\frac{B_{12} - A_{12}m }{A_{22}} \right) = B_{11}\\ A_{11}m + \frac{A_{12} B_{12}}{A_{22}} - \frac{A_{12}^2 m}{A_{22}} = B_{11}\\ \left(A_{11} - \frac{A_{12}^2 }{A_{22}}\right)m + \frac{A_{12} B_{12}}{A_{22}} = B_{11}\\ \Rightarrow m = \frac{\left(B_{11} - \frac{A_{12} B_{12}}{A_{22}}\right)}{\left(A_{11} - \frac{A_{12}^2}{A_{22}}\right)} \end{gather*}\end{split}\]

olarak buluruz.

Artık m’yi bildiğimize göre, n’nin tanımında yerine koyarak, n’yi de elde ederiz:

\[\begin{equation*} n = \frac{B_{12} - A_{12}m }{A_{22}} \end{equation*}\]

Denklemlerin çıkarımı biraz karışık gelse bile, önemli olan sonuçlar, çıkarımlardan başınız ağrıdıysa, sadece son A ile B’lerin tanımları ve m ile n’in onlar cinsinden eşitliklerini bilin. Zira formüller artık elimizde olduğundan, birazdan aşağıda göreceğiniz gibi, her şeyi kolayca hesaplayacağız! 8)

x = np.arange(1.,6)
y = np.array([9.8818, 18.9612, 29.5044, 36.7874, 53.2063])

A11 = A12 = A22 = B11 = B12 = 0 # Hesaplanacak değerler
N = x.shape[0] # Kaç adet verimiz olduğu

for i in range(N):
    A11 = A11 + 2*x[i]**2
    A12 = A12 + 2*x[i]
    A22 = A22 + 2
    B11 = B11 + 2*x[i]*y[i]
    B12 = B12 + 2*y[i]
    
# Toplamlar hesaplandı bile! 8)
m = (B11 - (A12 * B12 / A22))  / (A11 - (A12**2 / A22))
n = (B12 - A12 * m) / A22 

print("m = {:.3f}".format(m))
print("n = {:.3f}".format(n))

# Artık verilerimize en yakın geçen 
# doğrunun denklemi elimizde olduğuna göre
# hem doğruyu, hem de deney verilerini birlikte
# çizdirelim

xx = np.linspace(0,6,100)
tt = m*xx + n

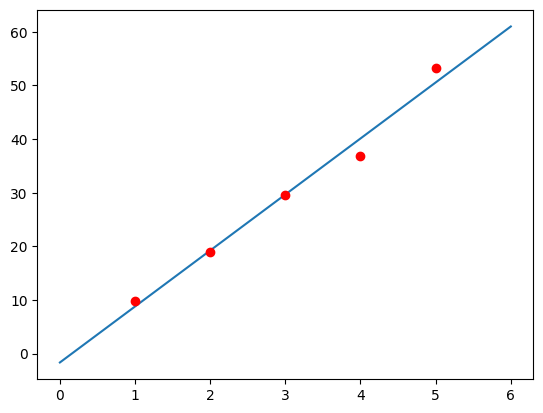
plt.plot(xx,tt,"-")
plt.plot(x,y,"ro")
plt.show()

m = 10.448
n = -1.674

Toplam vs. Skaler Çarpım

Konumuz döngülerin uygulaması olduğundan, en küçük kareler yöntemindeki toplamları döngü kullanarak yaptık ama bunun çok daha doğrudan bir yolu var: vektörlerin skaler çarpımı!

Hesaplattığımız toplamları hatırlayalım:

\[\begin{split}\begin{gather*} A_{11} = \sum_{i=1}^N 2x_i^2 ,\quad A_{12} = A_{21} = \sum_{i=1}^N 2x_i,\quad A_{22} = \sum_{i=1}^N 2\\ B_{11} = \sum_{i=1}^N 2x_i y_i,\quad B_{12} = \sum_{i=1}^N 2 y_i \end{gather*}\end{split}\]

Bu toplamlardan en karmaşık görünen \(B_{11}\) katsayısını \(\vec x\) ile \(\vec y\) vektörlerinin skaler çarpımının 2 katı olarak hesaplayabiliriz:

x = np.arange(1.,6)
y = np.array([9.8818, 18.9612, 29.5044, 36.7874, 53.2063])

B11 = 2*np.dot(x,y)
B11

1098.9969999999998

\(A_{11}\) ise \(\vec x\) vektörünün kendisi ile skaler çarpımının 2 katı:

A11 = 2*np.dot(x,x)
A11

110.0

\(A_{12}\) ve \(B_{12}\) vektörlerin bileşenlerinin toplamının 2 katı:

A12 = A21 = 2*np.sum(x)
B12 = 2*np.sum(y)
A12,B12

(30.0, 296.6822)

\(A_{22}\) katsayısı ise \(2\times N\)’den ibaret:

A22 = 2 * x.shape[0]
A22

10

Bulduğumuz bu katsayıları formülde yerlerine koyarak, \(m\) ve \(n\)’yi hesaplatıp, grafikleri tekrardan çizdirelim:

m = (B11 - (A12 * B12 / A22))  / (A11 - (A12**2 / A22))
n = (B12 - A12 * m) / A22 

print("m = {:.3f}".format(m))
print("n = {:.3f}".format(n))

# Artık verilerimize en yakın geçen 
# doğrunun denklemi elimizde olduğuna göre
# hem doğruyu, hem de deney verilerini birlikte
# çizdirelim

xx = np.linspace(0,6,100)
tt = m*xx + n

plt.plot(xx,tt,"-")
plt.plot(x,y,"ro")
plt.show()

m = 10.448
n = -1.674

numpy kütüphanesi, lineer cebir işlerinde yüksek hızda performans gösterecek şekilde tasarlandığından, doğrudan vektörler ve matrisler üzerinde işlem yapmak her zaman daha hızlı olacaktır. ;)