np.random.rand() vs. np.random.randint()#
Bu iki komutu öğrendiğimizden beri herhalde kullanmadığımız tek bir ders geçmemiştir çünkü gerçekten de o kadar önemliler fakat çağrılma ve çalışma şekilleri birbirlerinden çok farklı.
np.random.rand(boyut)#
np.random.rand() fonksiyonu 0 ile 1 arasında ondalıklı sayılar üretir. “-2 ile 5 arasında olsun” şeklinde sınırları belirtemezsiniz.
Eğer üretilen sayıların [a,b) aralığında olmasını istiyorsanız, bunu kendiniz yapmalısınız. rand(3,6) size 3 ile 6 arasındaki sayıları vermez, 3x6’lık bir matrisi 0 ile 1 arasında ondalıklı sayılarla doldurur. Aralığı kafamızı kullanarak biz modifiye ederiz, onu da şu şekilde yaparız:
x = np.random.rand() : 0 <= x < 1 : rand’ın normal aralığı, haydi bu eşitsizliği 9 ile çarpalım:
x = 9*np.random.rand() : 0 <= x < 9 : şimdi de her taraftan 2 çıkaralım:
x = 9*np.random.rand() -2 : -2 <= x < 7
Özetle: rand()’ı (b-a) ile çarpıp, (a) eklerseniz, üretilecek sayılar [a,b) aralığında olacaktır. rand()’ın parantezlerinin içine yazdığınız sayılar, boyut olarak ele alınacaktır.
a = 5 # alt sınır
b = 9 # üst sınır
N = 20 # boyut
np.random.rand(N)*(b-a) + a # üretilen sayılar a ile b arasında
array([7.65982334, 7.78157833, 7.53941586, 6.29677019, 6.16257943,
7.29302321, 8.89290938, 5.11936734, 8.58654053, 7.30944099,
8.08060591, 7.74042803, 7.73971949, 7.09547495, 6.8591284 ,
6.00287487, 7.97643299, 7.48885401, 5.37227004, 7.14214905])
a = 5 # alt sınır
b = 9 # üst sınır
m = 4 # satır adedi
n = 3 # sütun adedi
np.random.rand(m,n)*(b-a) + a # üretilen sayılar a ile b arasında
array([[6.6049681 , 6.6766348 , 6.81260754],
[7.39304722, 6.74157192, 7.96132158],
[6.26635478, 6.17236272, 7.73396033],
[5.52808826, 7.84645221, 5.88181361]])
np.random.randint(alt sınır (dahil), üst sınır (hariç), boyut)#
rand()’ın aksine, randint() sınır belirtmenize izin verir ve bu sınırlarda tam sayılar üretir (bunu hemen hepiniz biliyor ve uyguluyor zaten ama sorun rand()’ın da bu şekilde çalıştığını düşünmeniz).
a = 5 # alt sınır
b = 9 # üst sınır
N = 20 # boyut
np.random.randint(a,b,N) # üretilen sayılar a ile b arasında
array([6, 5, 7, 5, 6, 6, 6, 5, 5, 5, 5, 8, 5, 8, 7, 8, 8, 6, 6, 8])
a = 5 # alt sınır
b = 9 # üst sınır
m = 4 # satır adedi
n = 3 # sütun adedi
np.random.randint(a,b,(m,n)) # üretilen sayılar a ile b arasında
# 2 veya daha yüksek boyutlu matrislerde
# boyut parametrelerini parantez içerisinde
# kümeleriz.
array([[7, 8, 5],
[5, 8, 8],
[6, 8, 7],
[8, 5, 5]])
list.append() vs. np.append()#
Elinizde bir dizi var ve bu diziye eleman eklemek istiyorsunuz, bu noktada elinizdeki dizinin cinsi (tipi) yapacağınız işlemde büyük önem taşıyor. Bu noktada ya list.append() kullanacaksınız, ya da np.append(), ama hangisi, hangisi?
np.append()#
Dersimizde kullandığımız dizilerin hemen hemen hepsi numpy dizileri (np.array) fakat numpy dizilerinin “kötü” bir özelliği var ki, o da değiştirilemez (immutable) olmaları. numpy dizilerine eleman eklemeyi np.append() ile yapıyor görünsek de, aslında np.append’in yaptığı verilen iki diziyi (veya bir dizi ile değerleri) birleştirip, yeni bir dizi döndürmek! np.append uyguladığınız dizi aslında değişmeden kalır, o yüzden dönen sonucu bir değişkene (ki bu, asıl dizinin ta kendisi de olabilir) atamak.
dizi = np.array([1,2,3])
dizi
array([1, 2, 3])
dizi’nin sonuna 4 ekleyelim
np.append(dizi,4)
array([1, 2, 3, 4])
peki baştaki dizimiz değişti mi? (hayır)
dizi
array([1, 2, 3])
Değişmesi için np.append’in döndürdüğü değeri dizinin kendisine yönlendirelim:
dizi = np.append(dizi,4)
dizi
array([1, 2, 3, 4])
np.append böyle bir şey işte arkadaşlar (bir de np.concatenate() var, benzer işlemi yapıp dizileri birleştiren, o daha çok aynı boyuttaki dizileri birleştirmek için kullanılıyor).
list.append()#
Adi python listelerine eklemeyi sonlarına nokta koyup, append() metodunu çağırarak yaparız. Bu listeler esnek olduklarından, sorunsuz olarak ekleme işlemini yaparlar, np.append()’in aksine her seferinde yeni bir dizi oluşturmadıkları için de biriktirme amaçlı kullanıldıklarında çok daha hızlıdırlar. Bu türdeki listelere append ile doğrudan ekleme yapılır:
liste = [1,2,3]
liste
[1, 2, 3]
liste.append(4)
liste
[1, 2, 3, 4]
Yukarıdaki örnekte gördüğünüz üzere, ekleme sonucunda liste doğrudan uzadı. Eğer olur da, adi python listenizi numpy dizisine çevirmek isterseniz, bunu da doğrudan yapabilirsiniz:
type(liste)
list
liste = np.array(liste)
type(liste)
numpy.ndarray
liste
array([1, 2, 3, 4])
np.sum() biriktirme komutu değil!#
Sınavlarda sonuçlarınızı bir dizide biriktirmenizi istediğim sorularda özellikle “…sonuçlarınızı A adlı bir dizide toplayın” yazmaktan kaçınıyorum. Türkçe’de bildiğiniz üzere “toplamak” fiili hem aritmetik toplama işlemini (3 ile 5’i toplarsak 8 eder), hem de derleme eylimini (oyuncaklarını bu kutuda topladım) bünyesinde barındırmakta. Ben böyle dikkat edip soruları “…sonuçlarınızı A adlı bir dizide biriktirin” diye yazsam da, sonrasında cevaplarınızda nasıl oluyorsa dizinin elemanlarını matematiksel olarak toplatan np.sum() karşıma çıkıyor!
Bir dizideki 5’e bölünen sayıları içeren bir örnekle, ikisi arasındaki farkları gösterelim (spoiler alert: Dünya kadar fark varrrrr!!!)
Soru: Verilen dizi dizisindeki 5’e tam olarak bölünen sayıları bese_tam_bolunenler adındaki bir dizide biriktirin.
# Dizimizi tanımlayalım:
dizi = np.array([93, 15, 76, 64, 8, 77, 17, 88, 27,
20, 88, 37, 43, 69, 73, 66, 9, 43,
53, 82, 57, 42, 53, 4, 64, 79, 10,
92, 79, 76])
# Aranan sayıları biriktireceğimiz bese_tam_bolunenler dizisini
# boş olarak tanımlayalım ki, sonra ekleme yapabilelim
bese_tam_bolunenler = []
# Tek tek elemanların üzerinden giderek kontrolümüzü yapalım:
for i in dizi:
if(i%5 == 0):
bese_tam_bolunenler.append(i)
print(bese_tam_bolunenler)
[15, 20, 10]
Peki np.sum() ne yapar? Toplar.
np.sum(bese_tam_bolunenler)
45
np.dot() skaler çarpım operatörüdür!#
Kağıtlarınızda bir de şöyle bir şey sürekli gözüme çarptı (maalesef), iki vektör arasındaki açıyı hesapladığımızı düşünelim:
v1 = np.array([1,2,3])
v2 = np.array([4,5,6])
# skaler çarpımları
v1_dot_v2 = np.dot(v1,v2)
# boyları
v1_boy = np.linalg.norm(v1)
v2_boy = np.linalg.norm(v2)
aci = np.arccos(v1_dot_v2/(v1_boy*v2_boy))
print(np.rad2deg(aci))
12.933154491899135
Yukarıdaki kodda size garip bir şey yoktur umarım, ama bir de şuna bakın:
aci = np.arccos(v1_dot_v2/(np.dot(v1_boy,v2_boy)))
print(np.rad2deg(aci))
12.933154491899135
n boyutlu vektörleri, matrisleri aslanlar gibi bir çırpıda yapan np.dot()’a kalkıp da adi, bayağı, ilkokul çarpmasını dayadığınızda, efendiliğinden yine de yapıyor ama bu sizin python bilgileriniz konusunda pek çok şeyi de ele veriyor bir yandan.
3 * 5
15
np.dot(3,5)
15
Özet: yapmayın, yaptırmayın, ağlatmayın np.dot()’ı…
İşlem önceliği#
Size ortaokulda işlem önceliğini öğrettiklerinde aslında bu günlere hazırlıyorlardı, şimdi şu işlemi ele alalım:
Gayet kolay görünüyor değil mi (Cevap: 600/12=50 Bravo, bravo!)
Haydi gelin şimdi bunu python’da yapalım:
600 / 10 + 2
62.0
“Hocam, hiç öyle olur mu!” diyorsunuz, değil mi, işleri biraz zorlaştıralım, bu kaç:
600/20=30 (Süpersiniz!)
Bunu da python’da yapalım:
600 / 10 * 2
120.0
Sizler “Hocam, hiç öyle şey olur mu?” deyince, hoca da yapıştırmış cevabı: “O zaman şu aşağıdakini kim yazdı?”
np.dot(a,b) / np.linalg.norm(a) * np.linalg.norm(b)
Peki ya bu nasıl:
-b + np.sqrt(b**2-4*a*c) / 2 * a
olmuyormuş değil mi öyle yazınca… 8P 8(
Özet: Parantezler hayat kurtarır.
np.abs() düşündüğünüz şey değil.#
(Düşündüğünüz şey: np.linalg.norm())
Vektörlerin boyunu belirtmekte kullandığımız sembol ile mutlak değer sembolü birbirine benziyor, haklısınız, benzemelerinin de bir sebebi var zaten (vektörlerde de skalerlerde de orijine olan mesafeyi verirler) ama python’da bariz sebeplerden ötürü boy ölçme (np.linalg.norm()) ile mutlak değer alma (np.abs())işlemlerini farklı komutlarla yapıyoruz.
Bir vektör tanımlayıp, iki komutu da üstünde kullanalım:
v = np.array([-3,-4])
print("v: ",v)
print("np.abs(v): ",np.abs(v))
print("np.linalg.norm(v): ",np.linalg.norm(v))
v: [-3 -4]
np.abs(v): [3 4]
np.linalg.norm(v): 5.0
Sizin istediğiniz hangisi idi?
Bu arada, eğer np.linalg.norm’u hatırlayamadınız diyelim, vektörünün boyunun, elemanlarının karelerinin toplamının kökü olduğunu biliyorsunuz, o halde:
print(np.sqrt(np.dot(v,v)))
print(np.sqrt(np.sum(v*v)))
# hiçbir fonksiyon hatırlamıyorsanız
# bile döngü ile de yapabilirsiniz
boy = 0
for i in v:
boy = boy + i**2
print(np.sqrt(boy))
5.0
5.0
5.0
Vektörlerin açılarını genel olarak arctan ile bulamazsınız#
O iş sadece iki boyutlu vektörlerde geçerlidir, nedeninini bir düşünün bakalım… Genel olarak (kaç boyutlu olurlarsa olsunlar, boyutları birbirine eşit olduktan sonra) iki vektör arasındaki açı:
ile bulunur.
Vektörleri “o” şekilde tanımlamayı kimmmmm öğretti?????#
\(\vec a = 3\hat\imath-4\hat\jmath+2\hat k\) olsun, haydi bunu numpy’da tanımlayalım:
a = np.array([3,-4,2])
a
array([ 3, -4, 2])
bitti, bu kadar. Bizim normal notasyonda birim vektörlerle belirtmemiz, bileşenleri ayrı tutabilmek için, e bu zaten dizilerde otomatik olarak yapılıyor. Ama sınav kağıtlarınıza gelince:
i = np.array([1,0,0])
j = np.array([0,1,0])
k = np.array([0,0,1])
a = 3*i -4*j + 2*k
a
array([ 3, -4, 2])
Bu ne şimdi arkadaşlar? (bir, iki değil, onlarca arkadaş bu şekilde yapıyor)
Bilgisayarınızın içine silikon jel paketlerinden koyun çünkü siz böyle yaptıkça ağlıyor, gözyaşları rutubete, paslanmaya yol açar… (merak ediyorsanız, bu şekilde yazılmış kodları okurken ben de ağlıyorum, bilgisayarlarla birlikte ağlıyoruz…)
= vs. ==#
Python’da “=” sembolünün kullanıldığı tek bir yer vardır, o da atama işlemi. İşaretin sağındaki değeri, solundaki değişkene atar. Bu nedenle de sağında tanımlı bir değer, solunda da bir değişken olmalıdır (bariz ama gerçek).
a = 3 dediğinizde, “a” değişkeninin değerini 3 olarak tanımlar. Ardından b = a derseniz, öncesinde a’yı tanımlamış olduğumuz için, “b”nin değeri de 3 olur. Ama kalkıp c = d derseniz, ortada “d” diye bir değişken (ve onun tanımlı değeri) olmadığından hata alırsınız. Keza, 3 = a da 3’ün epey sağlam bir sabit (“değişmez”) olmasından ötürü, elinizde patlar. Benzer şekilde, bir şeyin karesini de doğrudan tanımlayamazsınız: omega**2 = g/lden anlamaz bilgisayar, o şekilde yapmak istiyorsanız, önce omega_kare = g/l dersiniz, sonrasında da omega = np.sqrt(omega_kare) diyebilirsiniz.
Özet: “=” işareti her zaman atama yapar.
Gelelim “==”e, bu da, kıyas operatörüdür, sağındaki ile solundaki aynı mı, ona bakar, döndüreceği şey ya “Doğru” ya “Yanlış” olur.
3 == 5 işleminin bilgisayarca okunuşu “3, 5’e eşittir” şeklinde bir önermedir, doğru olmadığından, bilgisayar da size “Yanlış” cevabını verir:
3 == 5
False
Bir şeyi tanımlamadan kullanamazsınız#
Bir önceki meseleyle alakalı olarak, 5. soruda elinizde \(\theta_max\) ve \(\varphi\) yokken (zaten onları bulmanız gerekiyordu) denklemlerinizde onları kullanamazsınız.
theta = theta_max*np.cos(omega*t+phi)
şeklinde yazdığınızda:
theta_max’ın,omega’nın,t’nin vephi’nin
ayrı ayrı tanımlanmış olması gerekir.
_Bu vesileyle,
şeklinde kod giremezsiniz, bu kadar kompleks hali bırakın, \(\pi\)’den bile anlamaz kompodor, açık açık np.pi yazmanız gerekmekte.
Sayı olmayan dizilerden seçim yapmak#
Taş-kağıt-makas sorusunda şu şekilde tanımlar vardı:
A = np.array(taş,kağıt,makas)
öyle olmaz, çünkü taş diye bir değişkeniniz yok, ama bu dertlerimizin en basitiydi, zira:
A = np.array(["taş","kağıt","makas"])
print(A)
['taş' 'kağıt' 'makas']
dersiniz, olur, biter. Sonrasında bunlardan birini rastgele seçmek istediğinizde hayalgücünüz sınır tanımamış.
np.random.rand(A,1): “A dizisinden 1 tane rastgele çek” demek değil, “bana hata ver” anlamına geliyor.np.random.randint(A,1): …
Bir diziden rastgele bir elemanı çekebilecek seviyedesiniz halbuki. Biraz düşünürseniz, ihtiyacınız olanın rastgele bir indis edinmek olduğunu fark edeceksiniz:
rastgele_indis = np.random.randint(3)
print("Rastgele seçilen indis: ",rastgele_indis)
print("Buna karşılık gelen eleman: A[i] = ",A[rastgele_indis])
Rastgele seçilen indis: 1
Buna karşılık gelen eleman: A[i] = kağıt
Derste görmedik (random ve randint bile bu kadar kaosa sürükledi) ama merak ediyorsanız, bu işi doğrudan yapan komut np.random.choice(dizi,boyut):
np.random.choice(A)
'makas'
print(np.random.choice(A,2))
['kağıt' 'taş']
print(np.random.choice(A,(3,4)))
[['makas' 'kağıt' 'kağıt' 'makas']
['makas' 'taş' 'taş' 'taş']
['kağıt' 'taş' 'kağıt' 'kağıt']]
while ile if aynı şeyler değiller!#
while: for döngüsü ile if’in birleşiminden ortaya çıkar: verilen koşul doğru olduğu müddetçe bloğundaki kodu çalıştırır. if’i ise “bir atımlık while” gibi düşünebilseniz de (ki, yine pek çok arkadaş bu şekilde düşünebilmiş sınavda), yazıktır, yapmayın.
plt.plot(x,y)#
plt.plot() komutu ilk parametre olarak değişkeni, ikinci parametre olarak da karşılık gelen değerleri alır. Yani, örneğin \(y = x^2\) fonksiyonunun grafiğini çizdirecekseniz, önce x değerlerini, ardından y değerlerini yazarsınız: plt.plot(x,y) şeklinde, plt.plot(y,x) şeklinde değil (bunu çok kişi yanlış yapmış, nedenini bir türlü anlayamadım gerçekten).
x = np.linspace(-2,2,100)
y = x**2
plt.plot(x,y)
plt.show()
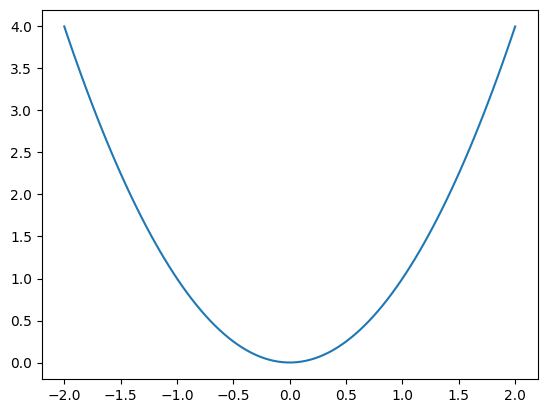
(bu vesileyle, np.linspace() oturmuş gibi, ona sevindim, teşekkür ederim 8) Bir teşekkür de soruda verilen değerleri girerken, birimlerini de yorum olarak (örn. g = 9.81 # m/s^2) not ettiğiniz için - inanın sizi ileride birçok dertten kurtaracak!).
Son Söz#
Arkadaşlar, ikinci sınavın özellikle ilk üç sorusu, sizlere bol puan kazandırmayı amaçlıyordu. Eğer bu üç soruyu yapamıyorsanız, bence bu dersten gerekli bilgileri almamışsınız demektir. 4. ve 5. sorular normal seviye sorularıydı (4. soru genel bir bilgisayar programlama sorusu; 5. soru ise olası bir fizik problemini bilgisayar kullanarak çözüp çözemeyeceğinizi anlamaya yönelikti: 5. soruda bilgisayarı hesap makinesi olarak kullanıyorsunuz aslında).
Genel sınavda soruları lütfen pas geçmeyin, elinizden geldiğince üzerlerinde uğraşın, başlamak bitirmenin yarısı olmasa da, epey bir puan alabiliyorsunuz, örneğin 5. soruda şu aşağıdaki kodu yazanlar 20 üzerinden 7 puan aldı:
M = 0.5 # kg
L = 1.0 # m
g = 9.81 # m/s^2
theta_0 = -np.pi/6 # rad
w_0 = 0.1 # rad/s
# yukarısı 3 puan!
w = np.sqrt(g/L) # bu satır 2 puan!
T = 2*np.pi/w # bu satır da 2 puan!
değerlerin girilmesi: 3 puan
açısal frekansın hesabı: 2 puan
periyotun hesabı: 2 puan
Henüz genel sınav sorularını hazırlamadım ama bu dersi alan bir öğrenci olsam, hocanın dönüp dönüp diziler, dizilerin işlenmesi, filtrelenmesi, vektörlerin arasındaki açılar, bulunanların bir listede biriktirilmesi konularından sorular sorduğunu fark ederdim (tabii ki garantisi yok ama olasılık denilen bilimsel bir faktör var! 8). Lütfen bilgisayar başında çalışın, kodlarınızı kendiniz yazın, tabii ki hata alacaksınız, bu çok normal ama en etkin yöntem bu şekilde çalışmak. Yapabiliyorsanız arkadaşlarınızla bir araya gelip bilgisayarda çalışın, grup çalışması da çok kazandırır.
Sınavlarınızda başarılar diliyorum, sağlıcakla kalın!
