1#
a,b ve c değişkenlerine [-5.5,5.5] aralığında rastgele (ondalık) değerler atayın ve bu değerleri ekrana yazdırın. Sonrasında,
formülünden \(ax^2+bx+c=0\) denkleminin köklerini hesaplatıp ekrana yazdırın. Formülü kullanmadan önce \(b^2-4ac\ge0\) eşitsizliğinin sağlandığını kontrol edip, eğer sağlanmıyorsa kök bulma işlemine geçmeyip ekrana “Gerçek kök yoktur” yazdırıp, programı sonlandırın (yani kökleri hesaplattırmadan bitirin).
(a,b,c) = np.random.rand(3)*11-5.5
print(a,b,c)
Delta = b**2-4*a*c
if(Delta<0):
print("Gerçek kök yoktur")
else:
x1 = (-b + np.sqrt(Delta))/(2*a)
x2 = (-b - np.sqrt(Delta))/(2*a)
print(x1,x2)
#print(np.roots([a,b,c]))
-3.3413544773579575 2.9293000488538325 4.227900067251298
-0.7689159155269137 1.6455963362077088
2#
Değerleri [-10,10] aralığında değişen rastgele ondalıklı sayılardan (100 x 2)’lik bir ‘noktalar’ matrisi oluşturun. Bu matrisin her satırı bir noktanın x ve y koordinatlarına karşılık gelmektedir. Matristeki noktalardan orijine (0,0) 5 birimden daha yakın olanlarının indis numaralarını ‘yakinlar’ adındaki bir dizide biriktirin.
noktalar = np.random.rand(100,2)*20-10
# 'Uzun' yol
yakinlar = []
for i in np.arange(noktalar.shape[0]):
if(np.sqrt(noktalar[i,0]**2 + noktalar[i,1]**2)<5):
yakinlar.append(i)
print(yakinlar)
[0, 11, 17, 18, 24, 33, 35, 40, 51, 53, 56, 57, 70, 72, 74, 89, 93, 96]
# 'İnce' yol:
mesafeler = np.linalg.norm(noktalar,axis=1)
#print(mesafeler)
yakinlar = np.arange(noktalar.shape[0])[mesafeler<5]
print(yakinlar)
[ 0 11 17 18 24 33 35 40 51 53 56 57 70 72 74 89 93 96]
3#
\(\vec a = -2\hat\imath + 3\hat\jmath - \hat k\) ile \(\vec b = 3\hat\imath + 2\hat\jmath + 5\hat k\) vektörleri arasındaki açıyı hesaplayın.
a = np.array([-2,3,-1])
b = np.array([3,2,5])
aci = np.rad2deg(np.dot(a,b)/(np.linalg.norm(a)*np.linalg.norm(b)))
print(aci)
-12.42043540686238
4#
Taş-Kağıt-Makas oyunu, iki oyuncunun aynı anda bu üç seçenekten birini seçip söylemesiyle oynanır: taş, makası; makas, kağıdı; kağıt ise taşı yener.
Bilgisayara kendisiyle 50 kere taş-kağıt-makas oynattırın. Oyuncular her turda rastgele olarak bu üç seçenekten birini seçip söylesinler, kazandıkları durumda 1 puan, beraberlik veya kaybettikleri durumda 0 puan alsınlar.
a) Her bir oyunda ne söylediklerini ekrana yazdırın; sonrasında duruma göre “1. oyuncu kazandı”, “2. oyuncu kazandı” veya “Berabere kaldılar” yazılsın.
b) 50 turun sonunda iki oyuncunun da toplam skorunu yazdırın.
# 'Uzun' yol
skor_1 = 0
skor_2 = 0
tkm = ['taş','kağıt','makas']
for i in np.arange(50):
oyuncu_1 = tkm[np.random.randint(0,3)]
oyuncu_2 = tkm[np.random.randint(0,3)]
print(i,". Tur: ",oyuncu_1," x ",oyuncu_2)
if(oyuncu_1 == "taş"):
if(oyuncu_2 == "kağıt"):
skor_2 += 1
print("2. oyuncu kazandı.")
elif(oyuncu_2 == "makas"):
skor_1 += 1
print("1. oyuncu kazandı.")
else:
print("Berabere kaldılar.")
elif(oyuncu_1 == "kağıt"):
if(oyuncu_2 == "makas"):
skor_2 += 1
print("2. oyuncu kazandı.")
elif(oyuncu_2 == "taş"):
skor_1 += 1
print("1. oyuncu kazandı.")
else:
print("Berabere kaldılar.")
else:
# 1. oyuncu makas
if(oyuncu_2 == "taş"):
skor_2 += 1
print("2. oyuncu kazandı.")
elif(oyuncu_2 == "kağıt"):
skor_1 += 1
print("1. oyuncu kazandı.")
else:
print("Berabere kaldılar.")
print("----------------------")
print(skor_1," :: ",skor_2)
0 . Tur: makas x makas
Berabere kaldılar.
----------------------
1 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
2 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
3 . Tur: taş x taş
Berabere kaldılar.
----------------------
4 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
5 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
6 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
7 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
8 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
9 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
10 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
11 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
12 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
13 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
14 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
15 . Tur: makas x makas
Berabere kaldılar.
----------------------
16 . Tur: taş x taş
Berabere kaldılar.
----------------------
17 . Tur: makas x makas
Berabere kaldılar.
----------------------
18 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
19 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
20 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
21 . Tur: kağıt x kağıt
Berabere kaldılar.
----------------------
22 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
23 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
24 . Tur: taş x taş
Berabere kaldılar.
----------------------
25 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
26 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
27 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
28 . Tur: taş x taş
Berabere kaldılar.
----------------------
29 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
30 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
31 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
32 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
33 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
34 . Tur: makas x makas
Berabere kaldılar.
----------------------
35 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
36 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
37 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
38 . Tur: taş x taş
Berabere kaldılar.
----------------------
39 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
40 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
41 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
42 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
43 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
44 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
45 . Tur: taş x taş
Berabere kaldılar.
----------------------
46 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
47 . Tur: taş x taş
Berabere kaldılar.
----------------------
48 . Tur: taş x taş
Berabere kaldılar.
----------------------
49 . Tur: makas x makas
Berabere kaldılar.
----------------------
17 :: 19
# 'İnce' yol
skor_1 = 0
skor_2 = 0
tkm = ['taş','kağıt','makas']
OlasiOyunSkoru = np.array([[[0,0],[0,1],[1,0]], # t-t,t-k,t-m
[[1,0],[0,0],[0,1]], # k-t,k-k,k-m
[[0,1],[1,0],[0,0]]]) # m-t,m-k,m-m
OlasiOyunSonucu=np.array([[0,2,1],
[1,0,2],
[2,1,0]])
Sonuclar = ['Berabere kaldılar.','1. oyuncu kazandı.','2. oyuncu kazandı.']
for i in np.arange(50):
oyuncu_1 = np.random.randint(0,3)
oyuncu_2 = np.random.randint(0,3)
skor_1 += OlasiOyunSkoru[oyuncu_1,oyuncu_2][0]
skor_2 += OlasiOyunSkoru[oyuncu_1,oyuncu_2][1]
print(i,". Tur: ",tkm[oyuncu_1]," x ",tkm[oyuncu_2])
print(Sonuclar[OlasiOyunSonucu[oyuncu_1,oyuncu_2]])
print("----------------------")
print(skor_1," :: ",skor_2)
0 . Tur: makas x makas
Berabere kaldılar.
----------------------
1 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
2 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
3 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
4 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
5 . Tur: makas x makas
Berabere kaldılar.
----------------------
6 . Tur: kağıt x kağıt
Berabere kaldılar.
----------------------
7 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
8 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
9 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
10 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
11 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
12 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
13 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
14 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
15 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
16 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
17 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
18 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
19 . Tur: taş x taş
Berabere kaldılar.
----------------------
20 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
21 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
22 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
23 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
24 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
25 . Tur: makas x makas
Berabere kaldılar.
----------------------
26 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
27 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
28 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
29 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
30 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
31 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
32 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
33 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
34 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
35 . Tur: makas x kağıt
1. oyuncu kazandı.
----------------------
36 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
37 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
38 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
39 . Tur: taş x taş
Berabere kaldılar.
----------------------
40 . Tur: taş x taş
Berabere kaldılar.
----------------------
41 . Tur: taş x taş
Berabere kaldılar.
----------------------
42 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
43 . Tur: kağıt x taş
1. oyuncu kazandı.
----------------------
44 . Tur: taş x makas
1. oyuncu kazandı.
----------------------
45 . Tur: taş x kağıt
2. oyuncu kazandı.
----------------------
46 . Tur: kağıt x makas
2. oyuncu kazandı.
----------------------
47 . Tur: makas x makas
Berabere kaldılar.
----------------------
48 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
49 . Tur: makas x taş
2. oyuncu kazandı.
----------------------
20 :: 21
5#
M = 0.5 kg kütleli bir cisim, L = 1 m uzunluğunda bir ipe asılarak bir sarkaç oluşturulmuştur. Küçük açı yaklaşımıyla, \(\omega=\sqrt{g/L}\) açısal frekansı olmak üzere, hareket denklemi \(\theta(t) = \theta_{max} \cos(\omega t+\phi)\) olarak verilmektedir. Burada \(\theta_{max}\) salınımın genliği, \(\phi\) ise faz açısı olup, başlangıç koşullarından bulunmaktadır.
Başlangıç açısı \(\theta_0=-\tfrac{\pi}{6}\) rad ve ilk hızı \(\dot\theta_0 = 0.1\) rad/s olarak belirtilmiş sarkacın, \(\theta_{max}\) ve \(\phi\) parametrelerini bulup, açı-zaman ve hız zaman grafiklerini bir periyot boyunca 300 nokta kullanarak çizdiren kod yazın. ( g = 9.81 m/s2 alın ve aman dikkat edin: \(\theta_{max}\) başlangıç açısına eşit değil!)
M = 0.5 # kg
L = 1 # m
g = 9.81 # m/s^2
theta_0 = -np.pi/6 # rad
omega_0 = 0.1 # rad/s
omega = np.sqrt(g/L)
T = 2*np.pi/omega # Periyot
print(omega,T)
3.132091952673165 2.006066680710647
Açısal konum denkleminin zamana göre türevi bize açısal hız denklemini verir:
Başlangıç koşulları (\(t=0\)) uygulanırsa:
İkinci denklemi birinci denkleme böldüğümüzde:
phi = np.arctan(-omega_0/(omega*theta_0))
print(np.rad2deg(phi))
3.489410839946685
Artık elimizde \(\phi\) olduğundan, birinci veya ikinci denklemde yerine koyup \(\theta_{max}\)’ı da bulabiliriz:
theta_max = theta_0 / np.cos(phi)
print(theta_max)
-0.5245712971559564
normalde, genlikler pozitif olarak alınır, yani aslında arctan’ı uygulayıp \(\phi\)’yi 1. bölgede bulduğumuzda, aynı değerin 3. bölgede de \((\phi+\pi)\) bulunacağını göz önüne almalıyız ki, bu durumda \(\phi\) 183.489 derece olurdu ve buradan ilerleseydik:
phi_alternatif = np.arctan(-omega_0/(omega*theta_0)) + np.pi
print("phi_alternatif: ",np.rad2deg(phi_alternatif))
theta_max_alternatif = theta_0 / np.cos(phi_alternatif)
print("theta_max_alternatif: ",theta_max_alternatif)
phi_alternatif: 183.4894108399467
theta_max_alternatif: 0.5245712971559564
olarak bulunur, denklemimiz de fiziksel açıdan daha doğru olurdu. Ama sınav sorusu olduğundan, bu kadar ince eleyip sık dokumamış olmanız puan kaybettirmeyecektir ;)
Grafiğini çizdirirsek:
t = np.linspace(0,T,300)
theta_t = theta_max_alternatif*np.cos(omega*t+phi_alternatif)
theta_dot_t = -omega*theta_max_alternatif*np.sin(omega*t+phi_alternatif)
plt.plot(t,theta_t,"b-")
plt.xlabel("Zaman (s)")
plt.ylabel("Açısal konum (rad)")
plt.show()
plt.plot(t,theta_dot_t,"r-")
plt.xlabel("Zaman (s)")
plt.ylabel("Açısal hız (rad/s)")
plt.show()
plt.plot(t,np.rad2deg(theta_t),"b-")
plt.xlabel("Zaman (s)")
plt.ylabel("Açısal konum (derece)")
plt.show()
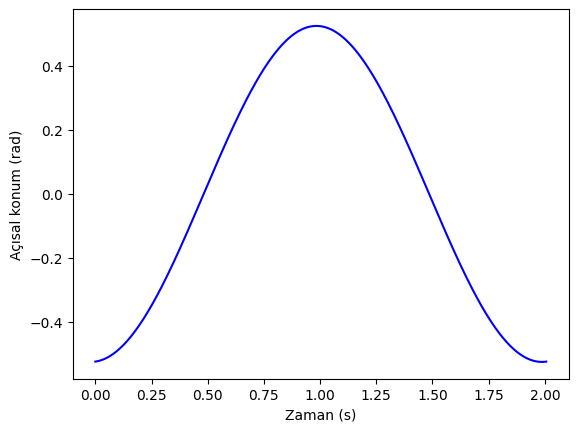
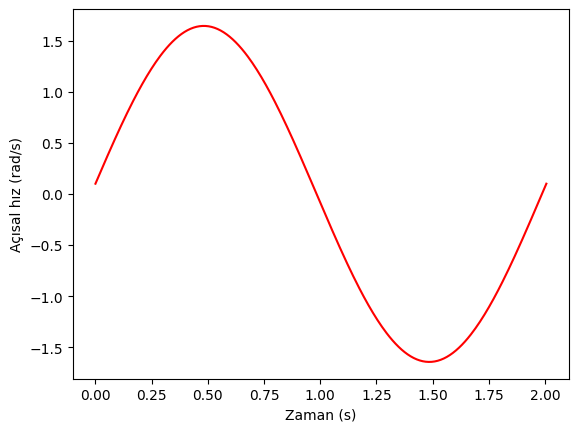
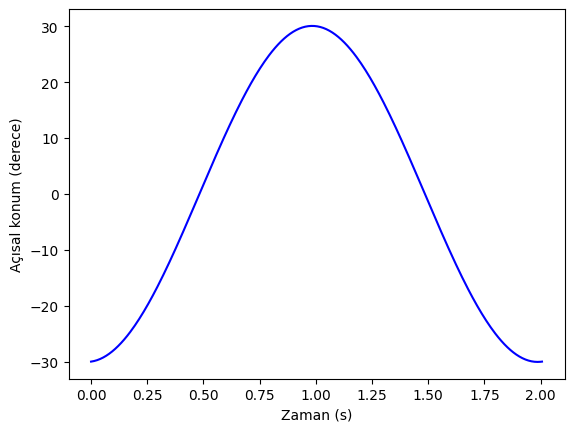
İlk hızımız sıfırdan farklı olduğundan, sarkaç başlangıç açısından \((\tfrac{\pi}{6}=30^o)\) daha fazla açı tarar:
th_max = np.max(theta_t)
print(th_max,np.rad2deg(th_max))
0.5245529367689089 30.05466940805122
