1#
Verilen \([a,b]\) aralığındaki bütün tamsayıların toplamını hesaplayan kod yazın.
Show code cell content
a = 5
b = 55 # diyelim (a ile b halihazırda verilmiş zira)
Show code cell content
# Çözüm 1_1
np.arange(a,b+1).sum()
1530
Show code cell content
# Çözüm 1_2
dizi = np.arange(a,b+1)
np.sum(dizi)
1530
Show code cell content
# Çözüm 2
toplam = 0
for i in range(a,b+1):
toplam = toplam + i
toplam
1530
2#
(100x2)’lik, her bir değeri -1 ile 1 arasında değişen (sınırları dahil de edebilirsiniz, dışarıda da bırakabilirsiniz, size kalmış) rastgele ondalıklı sayılardan oluşan bir ‘noktalar’ numpy dizisi oluşturun. Bu noktaların (0,0) noktasına olan uzaklıklarını hesaplatıp, sıralı olarak ‘mesafeler’ dizisinde toplayan kod yazın.
Show code cell content
noktalar = np.random.rand(100,2)*2 - 1
Show code cell content
# Çözüm 1
mesafeler = np.linalg.norm(noktalar,axis=1)
mesafeler
array([1.07499325, 0.24857006, 0.53011746, 0.33825794, 0.90244808,
0.65972132, 0.80867328, 0.55730627, 0.38318553, 0.94119047,
0.85986188, 0.59504123, 0.52640297, 0.55788273, 0.87590805,
1.03123663, 0.4234794 , 1.13049989, 0.49500217, 0.66923789,
0.8173986 , 0.62086787, 0.77607322, 0.3600567 , 0.97803954,
1.16464208, 0.6477279 , 1.24858846, 0.12776746, 0.73782905,
0.94352583, 0.79596316, 0.49766499, 0.78615852, 0.90252267,
1.28240098, 0.45298318, 0.66869709, 1.22194719, 0.8948793 ,
0.80072132, 0.90424402, 1.20478049, 1.2035012 , 0.43539162,
0.91891848, 0.95159324, 0.84195679, 0.94484373, 0.72068995,
0.66955766, 1.05708578, 0.72291408, 0.75386648, 0.41852303,
0.90526113, 0.81902264, 1.02310109, 0.69000516, 0.33265191,
0.29466093, 0.9470836 , 0.37427474, 1.17479613, 0.98635747,
0.83233749, 0.93868129, 0.83223256, 0.94929543, 0.95093888,
0.71430824, 0.89693135, 0.99666871, 1.19938781, 0.56926319,
1.06800668, 0.59521045, 0.42984011, 1.21592831, 0.67295735,
1.00060773, 1.24836194, 1.22605376, 0.63632507, 1.22150058,
0.81876005, 0.55086139, 0.25077739, 0.35889845, 1.01605379,
1.26484356, 0.19094141, 1.07764201, 0.63874168, 0.65430993,
1.04937475, 1.01561025, 0.32757134, 0.86172667, 0.51517267])
Show code cell content
# Çözüm 2
mesafeler = []
for nokta_no in range(100):
mesafe = np.sqrt(noktalar[nokta_no][0]**2 + noktalar[nokta_no][1]**2)
mesafeler.append(mesafe)
mesafeler
[1.0749932531532322,
0.24857006012700233,
0.5301174568979998,
0.3382579396431715,
0.9024480825402901,
0.6597213160756921,
0.8086732806686032,
0.557306273744699,
0.38318552650300874,
0.9411904741479746,
0.8598618810820522,
0.5950412254761865,
0.5264029723803276,
0.5578827336166285,
0.8759080523521708,
1.031236633665217,
0.4234794029232668,
1.1304998888895774,
0.49500216730944274,
0.6692378875225021,
0.8173985969082364,
0.620867874072519,
0.7760732231754672,
0.3600566975600102,
0.9780395407273278,
1.1646420825083845,
0.6477279016362029,
1.2485884553028694,
0.12776745528636171,
0.7378290546919072,
0.9435258298215249,
0.7959631626623935,
0.4976649932470249,
0.7861585232283559,
0.9025226653218213,
1.2824009752474388,
0.4529831774426424,
0.6686970880444807,
1.2219471923683043,
0.8948793022344547,
0.8007213202575266,
0.9042440207311784,
1.2047804895795526,
1.2035011984854858,
0.4353916245072016,
0.9189184794641451,
0.9515932445075661,
0.8419567911564683,
0.9448437330988667,
0.7206899468768239,
0.669557658551504,
1.057085775084724,
0.7229140759799426,
0.7538664812390713,
0.41852302610462133,
0.9052611319529201,
0.8190226394356356,
1.0231010901309237,
0.6900051575946105,
0.33265190776153336,
0.2946609303821488,
0.9470835955190158,
0.3742747432133454,
1.1747961293554265,
0.9863574749964108,
0.8323374942327499,
0.9386812864520837,
0.8322325626578744,
0.9492954265456318,
0.9509388754490776,
0.7143082438814035,
0.8969313537211883,
0.9966687091508356,
1.1993878092804187,
0.5692631923872371,
1.0680066812650506,
0.5952104526955956,
0.42984010616652507,
1.2159283077327283,
0.6729573471460032,
1.0006077311125603,
1.2483619436234492,
1.2260537570880463,
0.6363250656632813,
1.2215005751784074,
0.8187600534581477,
0.5508613912188493,
0.2507773888686439,
0.35889845424329375,
1.0160537893623225,
1.2648435619203455,
0.19094140601300835,
1.0776420109392846,
0.6387416767888818,
0.6543099270223515,
1.0493747505834994,
1.0156102532006415,
0.32757134474389404,
0.8617266709894644,
0.5151726714137445]
3#
Verilen bir numpy dizisinin elemanlarının karelerinin toplamını döndüren bir fonksiyon yazın.
Show code cell content
# Çözüm 1_1
def karetopla1_1(dizi):
return (dizi**2).sum()
# Çözüm 1_2
def karetopla1_2(dizi):
return np.sum(dizi**2)
# Çözüm 2
def karetopla2(dizi):
toplam = 0
for sayi in dizi:
toplam = toplam + sayi**2
return toplam
Show code cell content
# Üzerinde işlem yapacağımız bir dizi tanımlayıp,
# fonksiyonları çağıralım
dizimiz = np.array([3,6,1,-3.2])
print(karetopla1_1(dizimiz))
print(karetopla1_2(dizimiz))
print(karetopla2(dizimiz))
56.24
56.24
56.24
4#
Elimizde ne olduğu bizden gizlice tanımlanmış bir f(x) fonksiyonu var: fonksiyonun ne olduğunu bilmiyoruz ama mesela ‘f(5)’ deyince fonksiyonun \(x=5\) noktasındaki değeri geliyor. Dahası bize bu fonksiyonun sürekli, türevlenebilir ve \(x\in(-5,5)\) aralığında bir kökü olduğu belirtilmiş. Fonksiyonun kökünü bulan kod yazın.
(İpucu: Örneğin yarılama yöntemini kullanabilirsiniz)
Show code cell content
def f(x):
# Örnek fonksiyon
return np.cos(x) + x/5 + 0.6
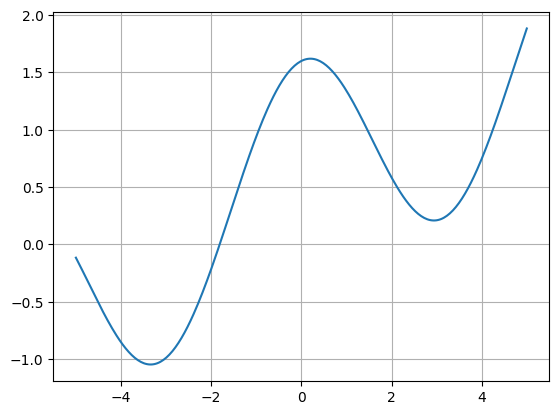
x = np.linspace(-5,5,300)
plt.plot(x,f(x),"-")
plt.grid(True)
plt.show()
Show code cell content
# Çözüm 1
hassasiyet = 1E-5
a = -5
b = 5
f_a = f(a)
f_b = f(b)
while(np.abs(a-b)>hassasiyet):
c = (a+b)/2
f_c = f(c)
if((f_c * f_a) < 0):
b = c
f_b = f_c
else:
a = c
f_a = f_c
print(c,f_c)
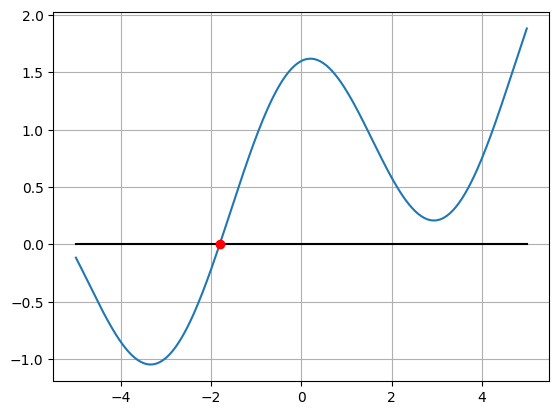
# İstenmemiş olsa da, grafikte tekrardan gösterelim:
plt.plot(x,f(x),"-")
plt.plot([-5,5],[0,0],"-k")
plt.plot(c,f_c,"ro")
plt.grid(True)
plt.show()
-1.810922622680664 -9.825057099011048e-06
Show code cell content
# Çözüm 2
hassasiyet = 1E-5
a = -5
f_a = f(a)
c = a + hassasiyet
f_c = f(c)
while((f_a*f_c)>0):
a = c
f_a = f_c
c = a + hassasiyet
f_c = f(c)
print(c,f_c)
-1.8109100000235165 4.959980466789915e-06
5#
Elimizde \(x\in [0,10]\) aralığında, düzgün sıralı \(10^6\) adet fonksiyon değeri var (‘x = np.linspace(0,10,1E6)’ yapmışız, sonrasında da ne olduğu bize söylenmeyen bu fonksiyonun o noktalardaki değerini hesaplatmışız gibi) – bu değerler ‘degerler’ numpy dizisinde tutuluyor olsun. Fonksiyonun türevini hesaplayıp çizdiren kod yazın.
Show code cell content
# Verileri üretmek için yine aynı örnek fonksiyonu kullanıp,
# sonrasında da unutalım.
def f(x):
# Örnek fonksiyon
return np.cos(x) + x/5 + 0.6
x = np.linspace(0,10,int(1E6))
degerler = f(x)
Show code cell content
# Çözüm
x = np.linspace(0,10,int(1E6))
# 'degerler' verilmiş durumda
delta_x = x[1] - x[0]
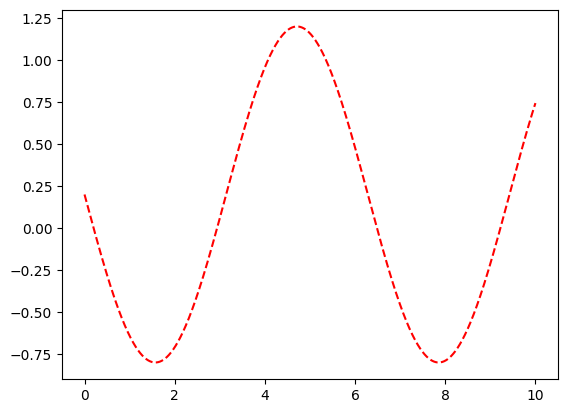
turev = (degerler[1:] - degerler[0:-1]) / delta_x
plt.plot(x[:-1],turev,"r--")
plt.show()
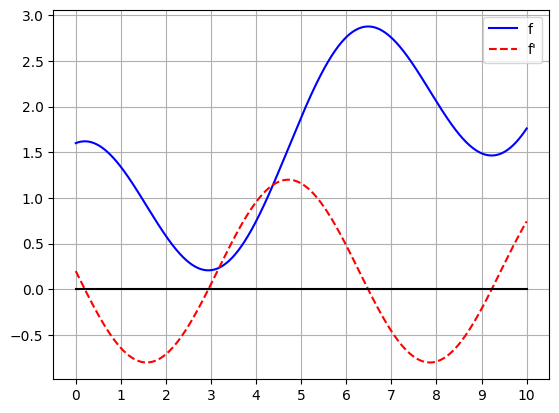
Ek olarak (soruda istenmemektedir, bilgi amaçlı olarak yapılmaktadır), türevin köklerinin gerçekten de fonksiyonun minimum/maksimum konumlarına denk geldiğini göstermek için değerlerle birlikte çizdirelim:
Show code cell content
plt.plot(x,degerler,"b-")
plt.plot(x[:-1],turev,"r--")
plt.grid(True)
plt.xticks(np.arange(0,10.01))
plt.plot([0,10],[0,0],"k-")
plt.legend(["f","f'"])
plt.show()