1#
20 x 30’luk, 1 ile 100 arasında (1 ile 100 dahil de olabilir, hariç de, size kalmış) rastgele sayılar içeren (sayılar tam sayı da olabilir, ondalıklı sayı da, bu da size kalmış), A ile B adında iki matris tanımlayın. Bu iki matrisin her bir hücresinin büyük olanını içeren bir C matrisi oluşturan kodu yazın.
Örnek: \(\underbrace{\begin{bmatrix}5&6\\3&1\end{bmatrix}}_{A}\oplus\underbrace{\begin{bmatrix}2&8\\2&5\end{bmatrix}}_{B}\Rightarrow\underbrace{\begin{bmatrix}5&8\\3&5\end{bmatrix}}_{C}\)
A = np.random.randint(1,100,(20,30))
B = np.random.randint(1,100,(20,30))
# Doğrudan, filtre kullanımı ile:
C = B.copy()
C[A>B] = A[A>B]
C[:3,:10]
array([[74, 99, 91, 35, 17, 64, 56, 96, 85, 48],
[52, 73, 89, 94, 95, 31, 22, 40, 90, 37],
[44, 47, 70, 55, 48, 62, 44, 59, 71, 72]])
# Döngü kullanıp, kıyaslayarak:
boyutlar = A.shape
C = np.zeros(boyutlar)
for i in range(boyutlar[0]):
for j in range(boyutlar[1]):
if (A[i,j] > B[i,j]):
C[i,j] = A[i,j]
else:
C[i,j] = B[i,j]
C[:3,:10]
array([[74., 99., 91., 35., 17., 64., 56., 96., 85., 48.],
[52., 73., 89., 94., 95., 31., 22., 40., 90., 37.],
[44., 47., 70., 55., 48., 62., 44., 59., 71., 72.]])
2#
a) denklem setini çözen komut/komutları yazın.
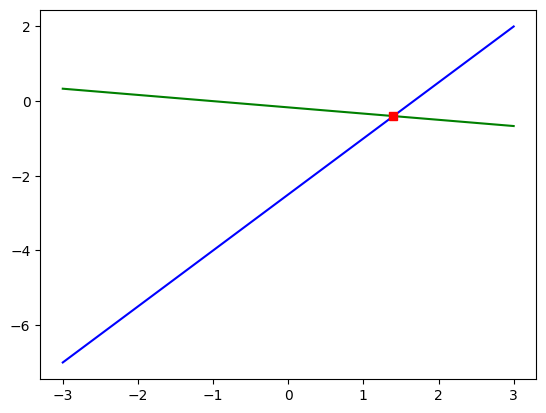
b) \(f(x)=\frac{3x-5}{2}\), \(g(x) = -\frac{x+1}{6}\) fonksiyonlarını [-3,3] aralığında en az 300 nokta kullanarak aynı grafik üzerinde çizdirin.
[Bonus: kesiştikleri noktayı da kırmızı bir kare olarak işaretleyin]
# a
A = np.array([[3,-2],[1,6]])
b = np.array([[5,-1]]).T
# solve() ile:
print(np.linalg.solve(A,b))
# katsayılar matrisinin tersiyle çarpmak sureti ile:
print(np.dot(np.linalg.inv(A),b))
xy = np.dot(np.linalg.inv(A),b)
[[ 1.4]
[-0.4]]
[[ 1.4]
[-0.4]]
# b
x = np.linspace(-3,3,300)
f = (3*x-5)/2
g = -(x+1)/6
plt.plot(x,f,"b-")
plt.plot(x,g,"g-")
plt.plot(xy[0,0],xy[1,0],"rs")
plt.show()
3#
a) Bileşenleri [-10,10] aralığında rastgele ondalıklı sayılar olan, iki adet 3 boyutlu vektör oluşturun, bunlara a ile b vektörleri diyelim.
b) Bu iki vektörün skaler çarpımını hesaplayın.
c) Bu iki vektör arasındaki açıyı derece cinsinden hesaplayın.
Bu iki vektörün vektör çarpımını hesaplayıp, buna c vektörü deyin (c = np.cross(a,b))
d) c vektörünün a ve b vektörlerine dik olduğunu gösterin.
# a
a = np.random.rand(3)*20-10
b = np.random.rand(3)*20-10
a,b
(array([ 4.93628889, -2.40209592, 9.88922901]),
array([-3.60344352, 6.18166789, 1.94102272]))
# b
s = np.dot(a,b)
s
-13.441379177068008
# c
cos_theta = s / (np.linalg.norm(a)*np.linalg.norm(b))
theta_rad = np.arccos(cos_theta)
theta_deg = np.rad2deg(theta_rad)
theta_deg
99.22372883703706
c = np.cross(a,b)
c
array([-65.79445219, -45.21672706, 21.85868151])
# d : doğrudan
# skaler çarpımlarının 0 olduğunu göstererek
np.dot(a,c),np.dot(b,c)
(-2.842170943040401e-14, 7.105427357601002e-15)
# d: aralarındaki açıyı hesaplayarak
cos_ac = np.dot(a,c) / (np.linalg.norm(a)*np.linalg.norm(c))
ac_rad = np.arccos(cos_ac)
ac_deg = np.rad2deg(ac_rad)
print("a : c",ac_deg)
cos_bc = np.dot(a,c) / (np.linalg.norm(b)*np.linalg.norm(c))
bc_rad = np.arccos(cos_bc)
bc_deg = np.rad2deg(bc_rad)
print("b : c",bc_deg)
a : c 90.0
b : c 90.0
4#
Her biri 50 elemanlı, [40, 290] aralığında, rastgele tam sayılardan oluşan iki dizi oluşturun (adları A ile B dizileri olsun). Bu iki dizinin ortak elemanlarını C adındaki bir dizide biriktiren kod yazın.
A = np.random.randint(40,291,50)
B = np.random.randint(40,291,50)
A,B
(array([240, 222, 218, 176, 264, 40, 250, 215, 109, 160, 262, 269, 61,
159, 51, 203, 46, 82, 217, 148, 147, 151, 106, 48, 182, 201,
219, 88, 177, 107, 104, 155, 56, 176, 269, 61, 173, 151, 183,
207, 173, 232, 87, 166, 169, 112, 272, 183, 128, 235]),
array([168, 120, 64, 41, 65, 91, 151, 62, 230, 252, 126, 286, 252,
221, 213, 63, 240, 95, 279, 114, 230, 103, 51, 122, 198, 109,
76, 77, 119, 146, 188, 285, 120, 96, 185, 88, 111, 264, 116,
244, 139, 85, 210, 247, 143, 260, 238, 175, 48, 172]))
# Döngülü, kontrollü çözüm
C = []
for i in range(A.size):
for j in range(B.size):
if (A[i] == B[j]):
if(A[i] not in C):
# Birden fazla aynı girişi
# önlemek için, çok lazım
# değil, bu son kontrolü
# koymasanız da sıkıntı
# olmaz. ;)
C.append(A[i])
C
[240, 264, 109, 51, 151, 48, 88]
# Filtreli, kontrollü
C = []
for i in range(A.size):
filtre = A[i] == B
if((B[filtre]).size>0):
C.append(B[filtre][0])
C
[240, 264, 109, 51, 151, 48, 88, 151]
# Tek komutla (bunu görmedik, referans olsun diye)
np.intersect1d(A,B)
array([ 48, 51, 88, 109, 151, 240, 264])
5#
tutulan_sayi değişkenine [1,100] aralığında rastgele bir tam sayı atayın. Bilgisayar bulana kadar tahmin etmeye çalışsın, tahmin tutulan sayıdan küçükse “çık”; büyükse “in” desin, bulunca kaç adımda bulduğunu da yazsın.
(Eğer akıllıca bir strateji kullanırsanız (ilk tahmini 50 olarak yaptırıp, sonra “in” derse 25, “çık” derse 75 olacak şekilde, gelen cevaba göre aralığı hep yarıladığınız şekilde) tam puan; “in”/”çık” cevaplarını çok önemsemezseniz yarım puan; hiç önemsemezseniz çeyrek puan üzerinden değerlendirilecektir)
tutulan_sayi = np.random.randint(1,101)
print("Tutulan sayı: ",tutulan_sayi)
print("----------------------\n\n")
flag_bulundu = False
tahmin = 50
kesin_min = 0
kesin_max = 101
i = 1
while(flag_bulundu == False):
print(i,". Tahmin: ",tahmin)
if(tahmin == tutulan_sayi):
print(i," Adımda Bulundu!")
break
elif(tahmin < tutulan_sayi):
print("çık")
kesin_min = tahmin
else:
print("in")
kesin_max = tahmin
tahmin = int(kesin_min + (kesin_max-kesin_min)/2)
i = i + 1
Tutulan sayı: 4
----------------------
1 . Tahmin: 50
in
2 . Tahmin: 25
in
3 . Tahmin: 12
in
4 . Tahmin: 6
in
5 . Tahmin: 3
çık
6 . Tahmin: 4
6 Adımda Bulundu!
