Grafik Çizimi#
Ders Notları: 3#
MatPlotLib ile Grafik Çizimi
Veriler
Markör çeşitleri
Renk çeşitleri
Markör boyu
Markörün iç ve dış renkleri
Çizgiler
Çizgi Çeşitleri
Çizgi Rengi
Çizgi kalınlığı
Gerekli şeyler & süs+püs
Başlıklar, tanımlar
“Izgara ve keneler” 8P
Grafiğin sınırları
Çoklu grafikler
Bir ipte iki cambaz (I)
Bir ipte iki cambaz (II)
Çok ipte çok cambaz
Saçılım
Histogram
3 Boyutlu Çizimler
Grafik çizimi: markör, renk, boy, çizgi çeşitleri; başlıklar, tanımlar, ızgara ve çentikler; grafiğin sınırları; çoklu grafikler; fonksiyon çizimi; saçılım; rastgele sayılar; saçılım grafiğinde 3. parametreye bağlı boy ve parlaklık farkı oluşturma; histogram; 3 boyutlu çizimler & kontür grafikleri; grafikleri dosyaya yazdırma.
Dr. Emre S. Taşcı, emre.tasci@hacettepe.edu.tr
Fizik Mühendisliği Bölümü
Hacettepe Üniversitesi
import numpy as np
import matplotlib.pyplot as plt
MatPlotLib ile Grafik Çizimi#
Veriler#
Elimizde, sınıf ortamında, yerden farklı yüksekliklerden bırakılan bir kütlenin düşme sürelerinin ölçüm verileri var:
Yükseklik (m) |
Düşüş Süresi (s) |
|---|---|
0.2 |
0.201900 |
0.7 |
0.377759 |
0.8 |
0.403882 |
1.2 |
0.494707 |
1.3 |
0.514983 |
1.8 |
0.606071 |
veriler = np.array([
[0.20000, 0.20190],
[0.70000, 0.37776],
[0.80000, 0.40388],
[1.20000, 0.49471],
[1.30000, 0.51498],
[1.80000, 0.60607]])
veriler
array([[0.2 , 0.2019 ],
[0.7 , 0.37776],
[0.8 , 0.40388],
[1.2 , 0.49471],
[1.3 , 0.51498],
[1.8 , 0.60607]])
y = veriler[:,0]
t = veriler[:,1]
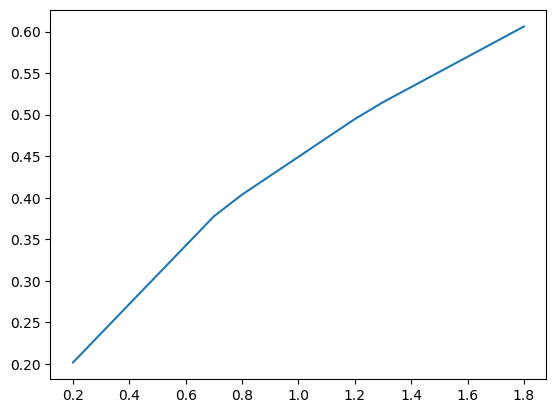
plt.plot(y,t)
plt.show()
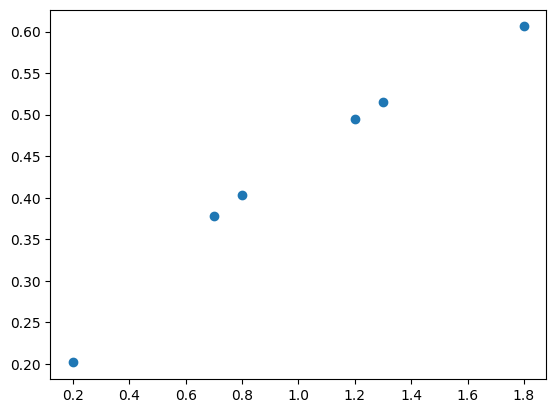
plt.plot(y,t,"o")
plt.show()
Markör çeşitleri#
Dilersek başka bir sürü şekil markör kullanabiliriz:
Sembol |
İşaret |
|---|---|
+ |
Artı |
o |
Daire |
* |
Yıldız |
. |
Nokta |
x |
Çarpı |
s |
Kare (square) |
d |
Paralelkenar/Elmas (diamond) |
^ |
Sivri ucu yukarıda olan üçgen |
v |
Sivri ucu aşağıda olan üçgen |
> |
Sivri ucu sağda olan üçgen |
< |
Sivri ucu solda olan üçgen |
p |
5 köşeli yıldız (pentagram) |
h |
6 köşeli yıldız (hexagram) |
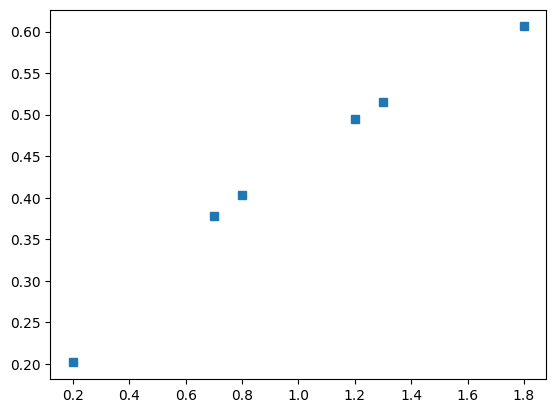
# Verileri karelerle temsil edelim:
plt.plot(y,t,"s")
plt.show()
Renk çeşitleri#
Renkleri hazır tanımlı renkler arasından belirtebiliriz (dilersek ‘color’ parametresi ile herhangi bir RGB üçlüsü olarak da belirtebiliriz, ama bu aşamada çok gerekli değil).
Hazır tanımlı renklerin listesine gelirsek:
Sembol |
Renk |
|---|---|
k |
Siyah (blacK) |
r |
Kırmızı (Red) |
g |
Yeşil (Green) |
b |
Mavi (Blue) |
m |
Mor (Magenta) |
c |
Turkuaz (Cyan) |
w |
Beyaz (White) |
Bu renk sembollerini de doğrudan markör sembolünün yanına yazıyoruz - çakışma olmadığı için hangisini önce yazdığımızın bir önemi yok, yeter ki aynı tırnak işaretinin içerisinde olsunlar: örneğin "xr" de, "rx" de, bize kırmızı çarpılı markörler çıkartır:
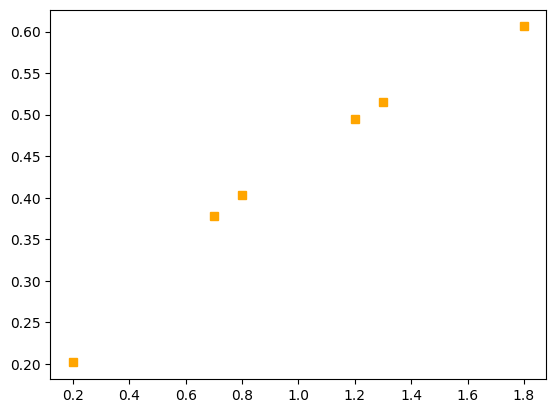
# Verileri karelerle temsil edelim:
plt.plot(y,t,"s",color="orange")
plt.show()
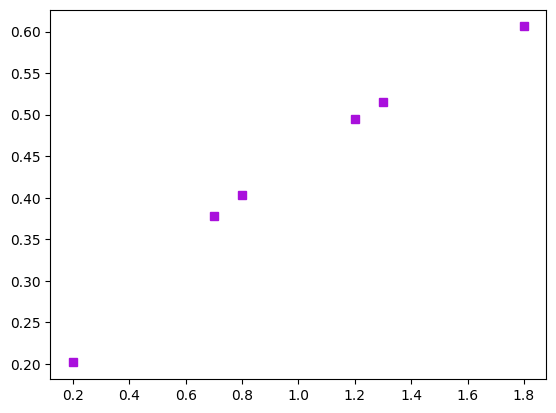
# Verileri karelerle temsil edelim:
plt.plot(y,t,"s",color="#a910dc")
plt.savefig("mor.png")
plt.show()
# Kırmızı çarpılar
plt.plot(y,t,"rx")
plt.savefig("/tmp/out.png",facecolor="white")
plt.show()
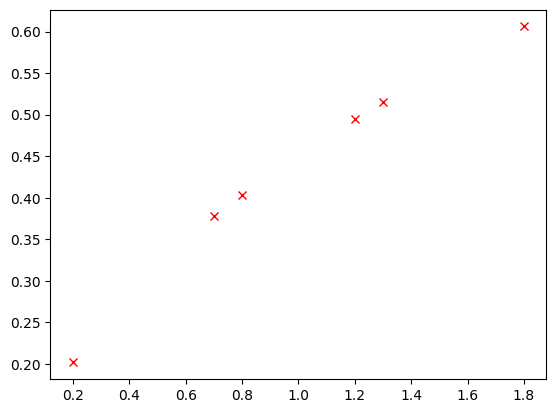
Markör boyu#
Çarpılar biraz küçük gibi görünüyor, büyütme işini "markersize" (markör boyu) parametresi ile yapıyoruz. Bu parametre markör şekli ve renginden biraz farklı bir şekilde tanımlanıyor yalnız: önce parametreyi girip, onu istediğim değere şu şekilde eşitliyoruz:
# Kırmızı büyük çarpılar
plt.plot(y,t,"rx",markersize=10)
plt.show()
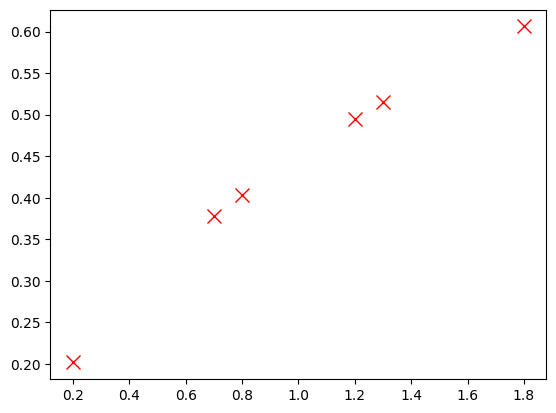
Markörün iç ve dış renkleri#
Eğer daire, kare veya yıldız gibi içi olan bir markör kullanıyorsak, içinin ve kontürünün renklerini sırasıyla "markerfacecolor" ve "markeredgecolor" parametreleriyle ayrı ayrı belirleyebiliriz.
Örneğin, içi yeşil, dışı kırmızı daireler kullanalım:
plt.plot(y,t,"o",markersize=10,
markerfacecolor="g",
markeredgecolor="r")
plt.show()
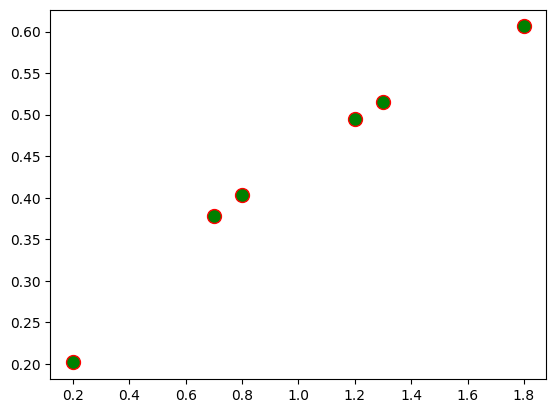
Çizgiler#
Markörleri iyice kavradığımıza göre, grafiklerimize biraz daha çeşitlilik katalım. Veri noktalarımızı çizgi ile birleştirmek için, biçim kısmına en temel halde bir - sembolü ekleriz:
plt.plot(y,t,"o-")
plt.show()
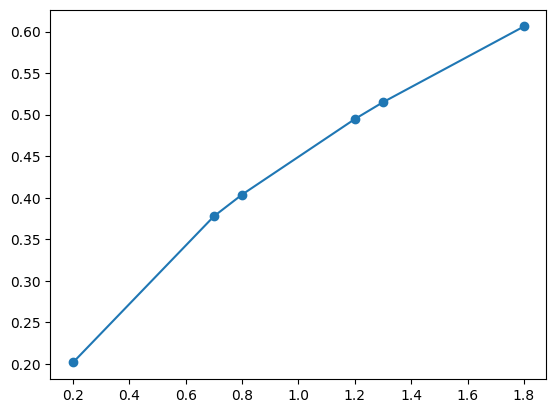
Çizgi Çeşitleri#
Her şeye olduğu gibi, çizgi biçimlerine de müdahale edebiliyoruz: çizgilerimizin çeşitlerini (düz, kesikli, nokta nokta, çizgi-nokta); rengini, kalınlığını, onlara karşılık gelen anahtar kelime / sembollerle ayarlayabiliriz.
Sembol |
Çizgi çeşidi |
|---|---|
- |
Düz çizgi |
– |
Kesikli çizgi |
: |
Nokta nokta |
-. |
Çizgi-nokta |
Nasıl göründüklerini altta topluca inceleyebilirsiniz (o 2x2 grafiği nasıl çizdirdiğimizi (subplot) de birazdan göreceğiz ;) :
plt.subplot(2,2,1)
plt.plot(y,t,"o-")
plt.title("Düz Çizgi")
plt.subplot(2,2,2)
plt.plot(y,t,"o--")
plt.title("Kesikli Çizgi")
plt.subplot(2,2,3)
plt.plot(y,t,"o:")
plt.title("Nokta nokta")
plt.subplot(2,2,4)
plt.plot(y,t,"o-.")
plt.title("Çizgi nokta")
plt.show()
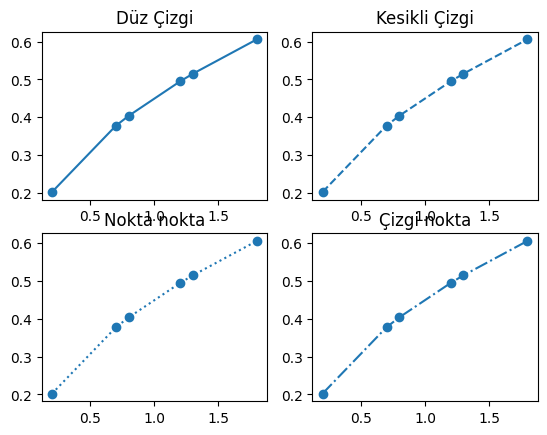
Çizgi Rengi#
Aslında en başından beri grafikleri çizerken, normal renk parametresi (örn. “or“‘deki “r”) olarak belirttiğimiz renk, temel olarak çizgi rengidir, markörlerin rengi de (“markerfacecolor” ve/veya “markeredgecolor” ile) aksi belirtilmedikçe bu renkte çizilir.
Yani, grafiğimizi mavi kesikli çizgi üzerine dışı kırmızı, içi yeşil dairesel markörlerle çizdirmek istersek, bunu şu şekilde yaparız:
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r")
plt.show()
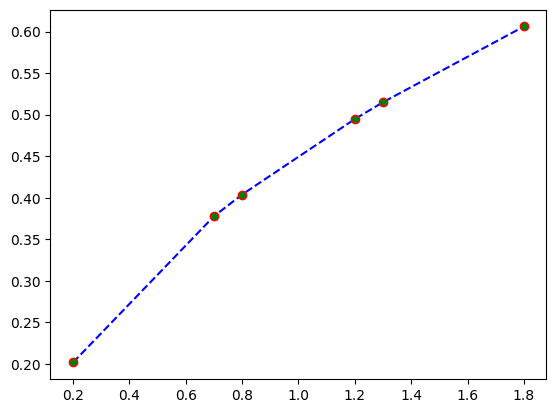
Çizgi kalınlığı#
Çizgi kalınlığını da linewidth parametresi ile belirtiriz. Yukarıdaki grafiği daha kalın çizgilerle çizmek için:
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4)
plt.show()
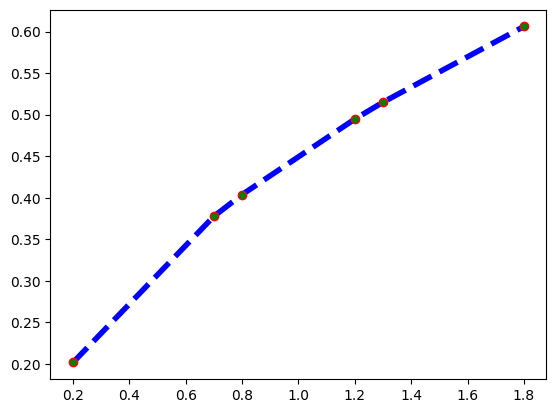
Markörler çizgilerin yanında biraz küçük kaldı, onları da coşturup, bu konuyu kapatalım:
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
plt.show()
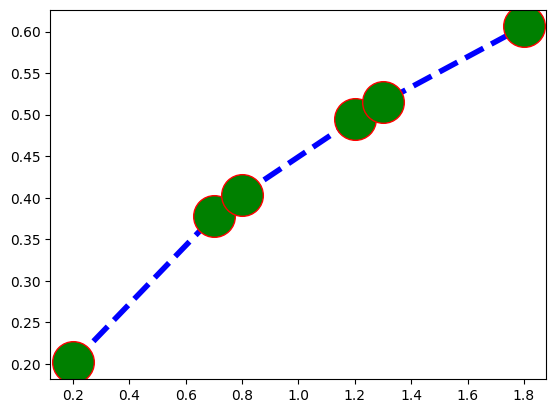
Gerekli şeyler & süs+püs#
Grafiklerimiz bu şekilde matematiksel olarak grafik olsalar da, fiziksel açıdan pek de işe yarar şeyler değiller: Neyin grafiği bu? Yatay ve düşey eksenler neyi temsil ediyor, birimleri nedir? Veri noktaları tam olarak neye karşılık geliyor? Bu noktada devreye grafik tanımlayıcıları girer.
Başlıklar, tanımlar#
Eksenlerin tanımlarını xlabel() ve ylabel() fonksiyonları ile ve grafiği plot ile çizdirdikten sonra belirtiriz. title() fonksiyonu ile de grafiğimizin başlığını yazarız. Örneğimiz üzerinde çalışalım, çok daha anlaşılır olacak:
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
#plt.title("Serbest Düşüş Deneyi")
plt.title(r"$a=-\frac{2y_0}{t^2}$'nın saptanması'")
plt.show()
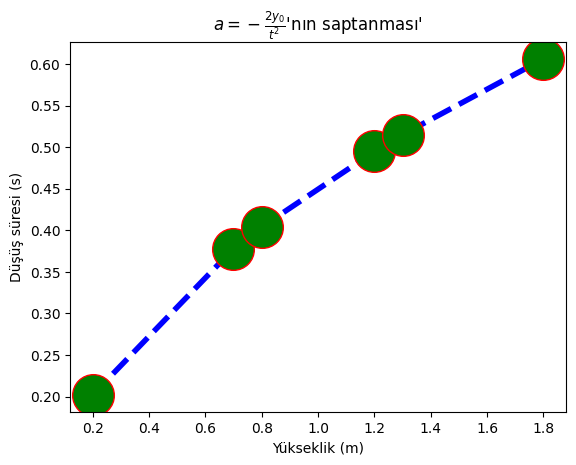
“Izgara ve keneler” 8P#
Grafik üzerindeki verilerimizin değerleri rahatça anlaşılıp, kıyaslanabilsin diye, eksenleri böldüğümüz aralıklardan çizgiler uzatırız. Bu kontrolü grid komutu ile gerçekleştiriyoruz:
grid(True)bu çizgilerin görüntülenmesini açargrid(False)da kapar
Eksenler üzerindeki hangi değerlerin hangi aralıklarla (örneğin yukarıdaki grafikte yatay eksen 0’dan 2’ye 0.5’lik aralıklarla; düşey eksen ise 0.2’den 0.7’ye 0.1’lik aralıklarla bölünmüş durumda) bölüneceğini, ya da bir başka deyişle çentik konumlarını ise sırasıyla xticks() ve yticks() fonksiyonları ile belirtiriz.
Yukarıdaki örnek üzerinde çalışmaya devam edersek, önce ızgarayı (grid’i) açalım:
# Grafiğimizi çizdiriyoruz
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
# Tanımlamaları yapıyoruz
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
# Izgarayı açalım
plt.grid(True)
plt.show()
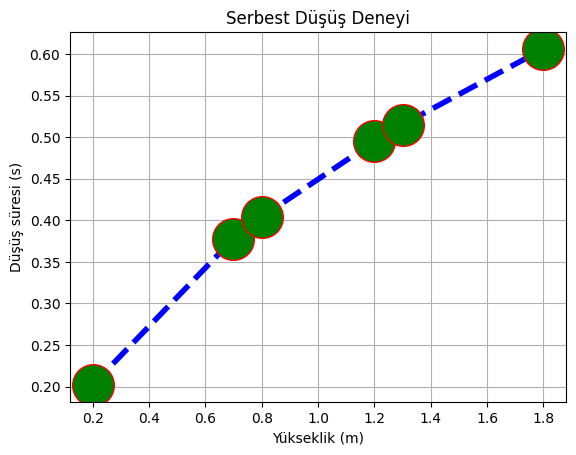
sonrasında da yatay ve düşey eksendeki çentikleri (ticks) sıklaştıralım:
# Grafiğimizi çizdiriyoruz
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
# Tanımlamaları yapıyoruz
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
# Izgarayı açalım
plt.grid(True)
# Çentikleri yeniden tanımlayalım
plt.xticks(np.arange(0,2.1,0.1))
plt.yticks(np.arange(0.2,0.73,0.025))
plt.show()
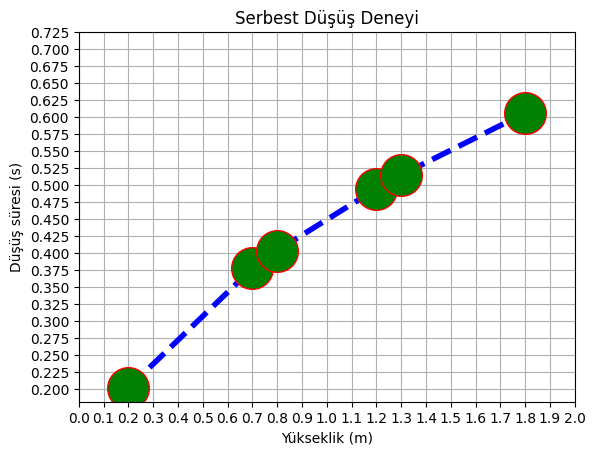
Grafik aynı grafik olsa da, okunabilirliği epey artmış oldu. Çentik tanımlamasını yaparken, aralık fonksiyonunu (np.arange()) kullandığımıza dikkatinizi çekerim.
Pek sık karşılaşılmasa da, çentikleri dilerseniz kafanıza göre, eşit olmayan aralıklarla da tanımlayabilirsiniz:
# Grafiğimizi çizdiriyoruz
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
# Tanımlamaları yapıyoruz
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
# Izgarayı açalım
plt.grid(True)
# Çentikleri yeniden tanımlayalım
# Yatay eksendekiler için sadece veri noktalarını
plt.xticks([0.2, 0.7, 0.8, 1.2, 1.3, 1.8])
# Düşey eksendekiler içinse kafamıza göre alalım...
plt.yticks([0.23,1/3,0.65])
plt.show()
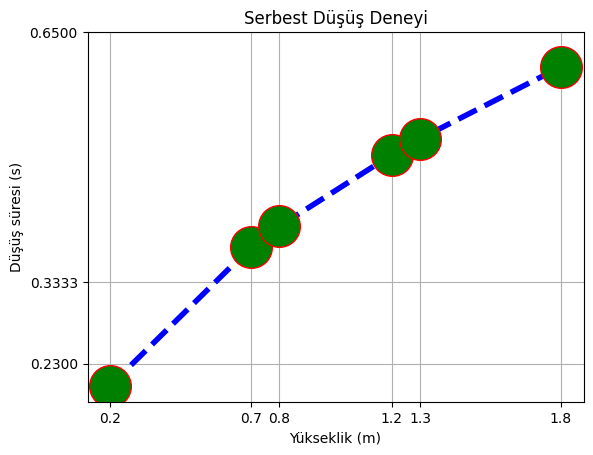
(tahmin edebileceğiniz üzere, yatay eksendeki çentikleri tek tek yazmak yerine, doğrudan xticks(y) de diyebilirdik - ne de olsa y değişkeni doğal olarak yukarıda girdiğimiz veri noktalarını tutmakta ;)
Grafiğin sınırları#
Grafiğimizin çizim sınırlarını axis() fonksiyonu ile belirliyoruz. Parametre olarak bir dizi alır ve dizinin eleman sayısı 2 ise bunlar yatay eksenin minimum ve maksimum değerlerini; 4 elemanlı bir dizi ise o zaman da dizinin elemanlarını sırasıyla yatay eksenin minimum ve maksimum değerleri ve düşey eksenin minimum ve maksimum değerleri olarak yorumlar.
Yukarıdaki örneğimizi önce bir düzgün çizdirelim:
# Grafiğimizi çizdiriyoruz
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
# Tanımlamaları yapıyoruz
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
# Izgarayı açalım
plt.grid(True)
plt.show()

Yatay eksenin gösterim aralığını [-1,3], düşey eksen aralığını ise [0,1] yapalım:
# Grafiğimizi çizdiriyoruz
plt.plot(y,t,"b--o",markerfacecolor="g",
markeredgecolor="r",
linewidth=4,
markersize = 30)
# Tanımlamaları yapıyoruz
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
# Izgarayı açalım
plt.grid(True)
plt.axis([-1,3,0,1])
plt.show()
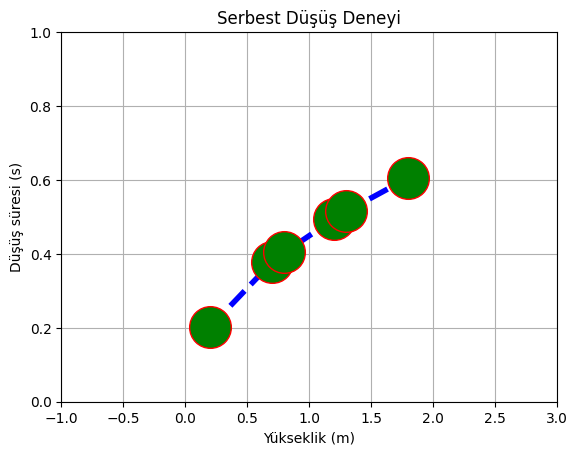
Çoklu grafikler#
Bir ipte iki cambaz (I)#
Bir grafik üzerinde iki veri setini göstermek için, sanki iki ayrı grafik çizdirecekmişiz gibi tanımlayıp, sonra bunları aynı plot() fonksiyonu içerisinde birleştiririz.
Ders boyunca kullanageldiğimiz veri setini hatırlayalım:
veriler
array([[0.2 , 0.2019 ],
[0.7 , 0.37776],
[0.8 , 0.40388],
[1.2 , 0.49471],
[1.3 , 0.51498],
[1.8 , 0.60607]])
Bu serbest düşüş deneyini ellerinde kronometre olmadığından, süreyi saatin saniye kısmıyla ölçen ikinci bir grubun da yapmış olduğunu ve şu sonuçları aldığını varsayalım:
veriler_2 = np.array([
[0.20000, 0.3],
[0.70000, 0.4],
[0.80000, 0.4],
[1.20000, 0.5],
[1.30000, 0.6],
[1.80000, 0.7]])
# 2. sütunu t_2 değişkenine atayalım
t_2 = veriler_2[:,1]
# (y değerleri (1.sütun) ilk veri setiyle
# aynı olduğundan, onu ayrıca bir y_2 değişkenine
# atamadık)
veriler_2
array([[0.2, 0.3],
[0.7, 0.4],
[0.8, 0.4],
[1.2, 0.5],
[1.3, 0.6],
[1.8, 0.7]])
İkisini ayrı ayrı çizdirecek gibi yapıyoruz ama plt.show() komutunu en sonda vererek aynı “tuval” üzerinde çıkmalarını sağlıyoruz:
plt.plot(y,t,"^-b") # 1. grafik
plt.plot(y,t_2,"o-r") # 2. grafik
plt.show()
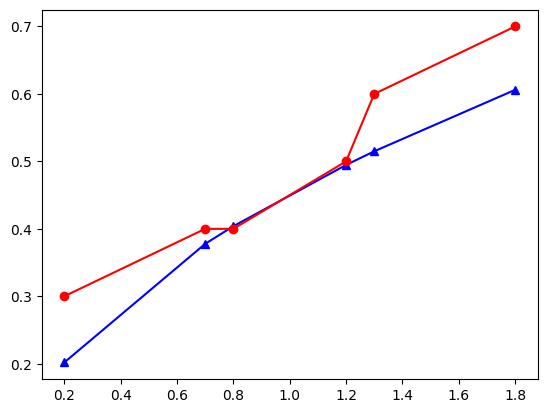
Hangisinin hangisi olduğunun açıklamasını ise legend() komutu ile belirtebiliriz (hazır yapıyorken, tanımları da koyalım):
plt.plot(y,t,"^-b") # 1. grafik
plt.plot(y,t_2,"o-r") # 2. grafik
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
plt.legend(["Hassas Ölçüm (1.Grup)","Kaba Ölçüm (2. Grup)"])
# Izgarayı da açalım
plt.grid(True)
plt.show()
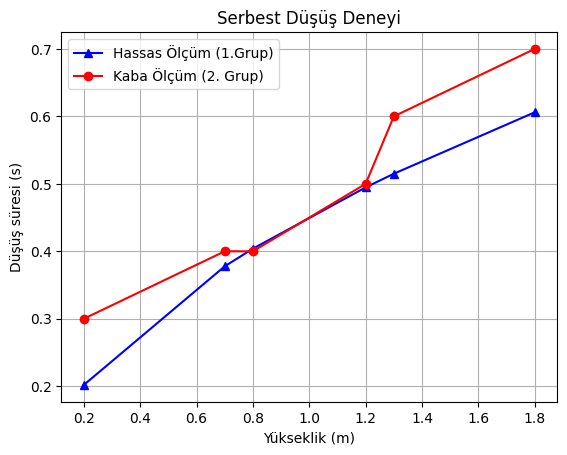
Açıklama kutusunun konumunu değiştirmek istersek, bunu da “loc” parametresi ile yapıyoruz. Parametre değerleri olarak merkez dahil 10 konum + verilerle çakıştırmadan iyi bir yere koyma işini bilgisayara bırakmak istiyorsak bir de “best” ile birlikte 11 değer kullanabiliyoruz:
'best' (0), 'upper right' (1), 'upper left' (2), 'lower left' (3), 'lower right' (4), 'right' (5), 'center left' (6), 'center right' (7), 'lower center' (8), 'upper center' (9), 'center' (10),
(parantez içindeki sayılar bölgelere karşılık gelip, onları da doğrudan değer olarak kullanabiliriz)
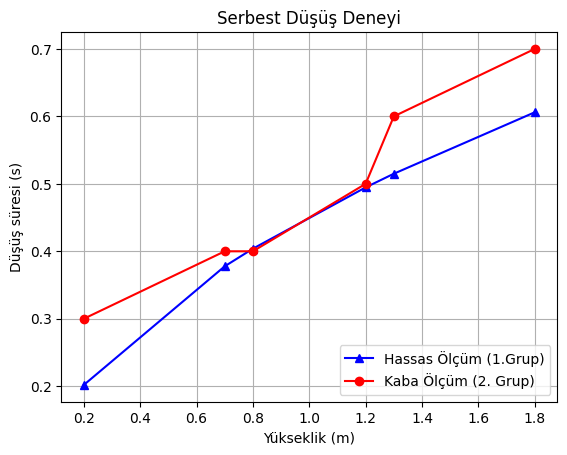
plt.plot(y,t,"^-b") # 1. grafik
plt.plot(y,t_2,"o-r") # 2. grafik
plt.xlabel("Yükseklik (m)")
plt.ylabel("Düşüş süresi (s)")
plt.title("Serbest Düşüş Deneyi")
plt.legend(["Hassas Ölçüm (1.Grup)","Kaba Ölçüm (2. Grup)"],
loc="lower right")
# Izgarayı da açalım
plt.grid(True)
plt.show()
Bir ipte iki cambaz (II)#
\(y=x\) ve \(y=x^2\) fonksiyonlarının grafiklerini \(x \in [0,1]\) aralığında çizdirmeyi deneyelim:
x = np.linspace(0,1,125)
y_1 = x
y_2 = x**2
plt.plot(x,y_1,linewidth=4)
plt.plot(x,y_2,linewidth=4)
plt.legend([r"$y=x$",r"$y=x^2$"],loc="best")
plt.show()
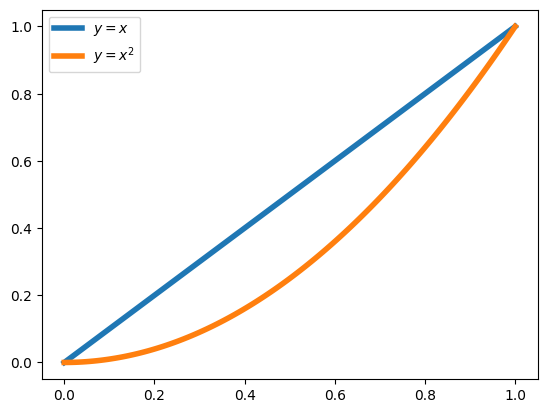
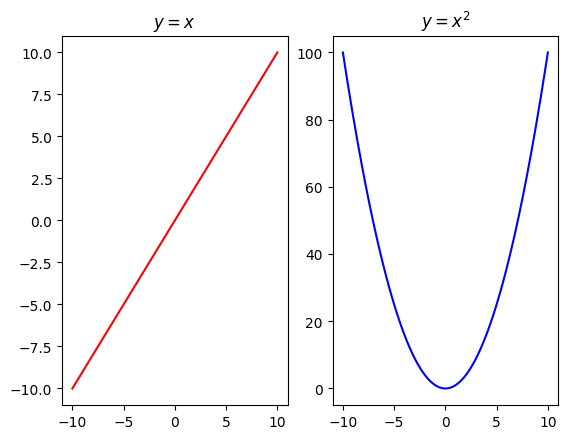
Şimdi bir de \(x \in [-10,10]\) aralığında çizdirmeyi deneyelim:
x = np.linspace(-10,10,250)
y_1 = x
y_2 = x**2
plt.plot(x,y_1,linewidth=4)
plt.plot(x,y_2,linewidth=4)
plt.legend([r"$y=x$",r"$y=x^2$"],loc="best")
plt.show()
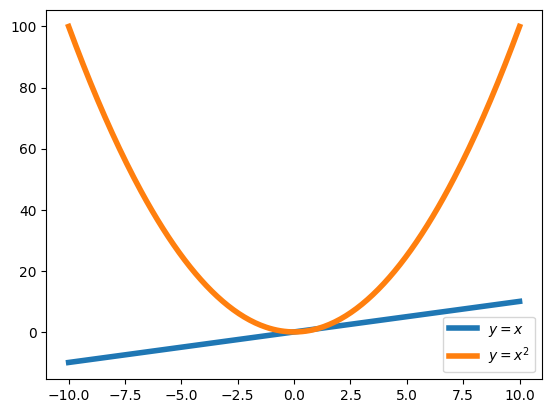
Bu grafikteki sorun nedir? \(x\), 0 ile 1 arasındayken iki grafiğin değerleri gayet güzel anlaşıyorlardı fakat aralık artınca, değerler arasındaki farklar da uçtu gitti, bu nedenle \(y_2 = x^2\) fonksiyonu baskın hale gelip, \(y_1 =x\) fonksiyonunu gölgeledi. Bu türden, farklı değer aralıklarına sahip fonksiyonları birlikte gösterebilmek için, iki farklı düşey eksen kullanmamızı sağlayan twinx() fonksiyonu ile çizim yaparız fakat ikinci grafiği birinci ile ilişkilendirmek için eksenlere isim atayıp, subplots() fonksiyonu ile ilerlememiz gerekmektedir.
x = np.linspace(-10,10,250)
y_1 = x
y_2 = x**2
fig,ax1 = plt.subplots()
ax1.plot(x,y_1,"b",linewidth=4)
ax1.set_ylabel(r"$x$", color="b")
ax1.tick_params(axis='y', color='blue', labelcolor='blue')
ax2 = ax1.twinx()
ax2.set_ylabel(r"$x^2$",color="orange")
ax2.plot(x,y_2,"orange",linewidth=4)
ax2.tick_params(axis='y', color='orange', labelcolor='orange')
ax2.spines['left'].set_color("blue")
ax2.spines['right'].set_color("orange")
fig.legend([r"$y=x$",r"$y=x^2$"],loc="lower right")
plt.show()
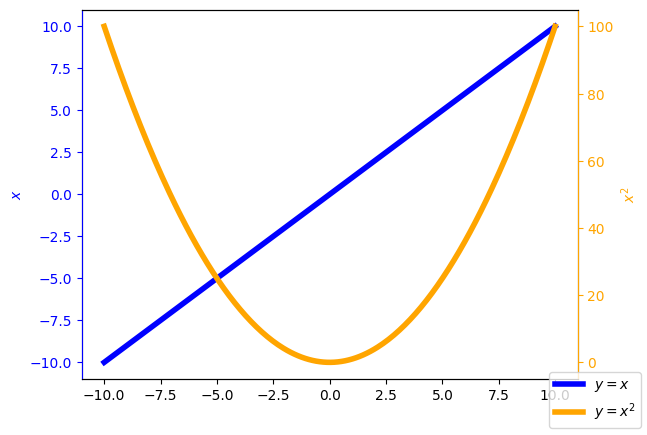
Çok ipte çok cambaz#
Artık grafik çizmeyi epey epey öğrendiğimize göre, aynı grafik tuvali üzerinde farklı grafikleri sıralamayı da görebiliriz. Bu sıralama işini subplot() komutu ile tanımlıyoruz.
Gözünüzün önüne (2x2)’lik bir matris getirin, örneğin:
olsun.
Matrise bir isim vermediğimizden, bir yeri belirtmek için, her seferinde matrisin boyutunu ve yerin indisini belirtiriz. Mesela sağ alt köşedeki elemanı belirtmek için “2’ye 2’lik bir matrisi gözünüzün önüne getirip, onun 4. elemanının yerini düşünün” demek gibi. İşte subplot()’un parametreleri de bu şekilde çalışıyor. Her birini ayrı ayrı belirtip, oraya ne koyacağımızı tanımlıyoruz sonra. Aşağıdaki örneklere bakarsanız çok daha açıklayıcı olacağını umut ediyorum:
# 1x2'lik bir düzen
plt.subplot(1,2,1)
# 1x2'lik matrisin 1. elemanı, yani soldaki penceredeyiz
plt.plot(x,y_1,"-r")
plt.title(r"$y=x$")
plt.subplot(1,2,2)
# şimdi 1x2'lik matrisin 2. elemanı, yani sağ penceredeyiz
plt.plot(x,y_2,"-b")
plt.title(r"$y=x^2$")
plt.show()
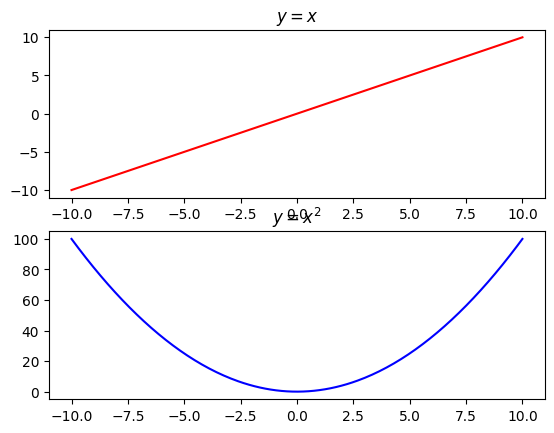
# 2x1'lik bir düzen
plt.subplot(2,1,1)
# 1x2'lik matrisin 1. elemanı, yani yukarıdaki penceredeyiz
plt.plot(x,y_1,"-r")
plt.title(r"$y=x$")
plt.subplot(2,1,2)
# şimdi 1x2'lik matrisin 2. elemanı, yani aşağıdaki penceredeyiz
plt.plot(x,y_2,"-b")
plt.title(r"$y=x^2$")
plt.show()
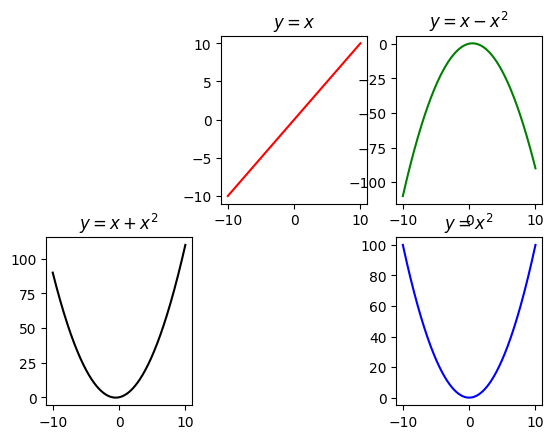
İlle de bütün hücreler dolacak diye bir kural da yok bu arada:
# 2x3'lük bir düzen
plt.subplot(2,3,2)
# 2x3'lik matrisin 2. elemanı, yani yukarı satır, orta sütun
plt.plot(x,y_1,"-r")
plt.title(r"$y=x$")
plt.subplot(2,3,3)
# 2x3'lük matrisin 3. elemanı, yani sağ-üst hücre
plt.plot(x,y_1-y_2,"-g")
plt.title(r"$y=x-x^2$")
plt.subplot(2,3,4)
# 2x3'lük matrisin 4. elemanı, yani sol-alt hücre
plt.plot(x,y_1+y_2,"-k")
plt.title(r"$y=x+x^2$")
plt.subplot(2,3,6)
# şimdi 2x3'lük matrisin 6. elemanı, yani sağ-alt hücre
plt.plot(x,y_2,"-b")
plt.title(r"$y=x^2$")
plt.show()
Saçılım#
Yukarıdaki örneklerdeki verilerimiz hep sıralı verilerdi, yani noktalarımızı art arda çizgilerle birleştirince anlamlı bir şekil elde ediyor, gelişim sürecini izleyebiliyorduk. Fakat saçılma deneyleri gibi deneylerde (ya da elinizdeki vişne suyu dolu bardağı beyaz halıya düşürdüğünüzde oluşan desenler gibi kazalarda) bu şekilde bir sıralılık aranmaz. Bu tür durumlarda, plot yerine scatter fonksiyonunu kullanmak birtakım avantajlar (farklı şekilde büyüklük ve renklendirme yapabilmek gibi) sunar.
Saçılım için genelde çok fazla veriye ihtiyaç duyulur. Vişne bardağımızı kare şeklinde halımızın tam ortasına düşürdüğümüzü ve 300 adet damlanın rastgele yönlere sıçradığını varsayalım.
Halımızın merkezini (0,0), boyunu da 4x4 \(m^2\) alırsak, üzerine rastgele şekilde dökülen 10 damlanın konumlarını (x,y) cinsinden şu şekilde üretebiliriz:
damlalar = np.random.rand(10,2)*4-2
damlalar
array([[-0.08290347, 0.37293478],
[ 0.84245215, 0.70923122],
[ 1.32473193, -0.50838017],
[-0.85037989, 0.23950027],
[-1.35359355, -0.17442058],
[ 1.60644663, 0.96597717],
[-0.88302421, -1.70303744],
[ 1.81956343, -0.46815935],
[-1.77267888, 1.27402676],
[-1.7945238 , 0.24753581]])
Çizdirmek için scatter’ı kullanalım:
plt.scatter(damlalar[:,0],damlalar[:,1],100)
plt.show()
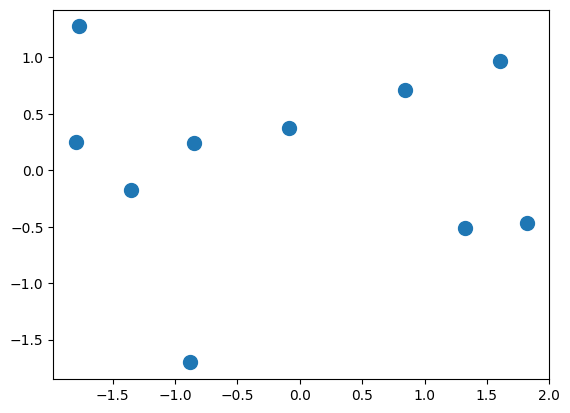
Yukarıdaki “100” parametresi boyla orantılı bir değer.
Damla sayısını 300’e çıkaralım:
damlalar = np.random.rand(300,2)*4-2
plt.scatter(damlalar[:,0],damlalar[:,1],100)
plt.show()
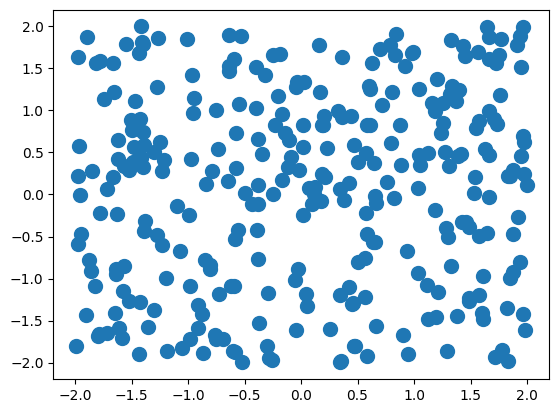
Kar beyaz halının ortasına dökülen vişne suyunun damlacıklarının konumu için düzgün dağılım çok da gerçekçi değil bu arada, sonuçta tahmin edebilirsiniz ki, normalde halının merkezine yakın düşen damlacıkların sayısı (/yoğunluğu) halının uçlarına kadar ulaşan damlacık sayısından (/yoğunluğundan) çok daha fazla olacaktır.
Burada “normalde” terimi anahtar kelimemiz. Doğada pek çok kez gözlemlediğimiz, belli bir ortalama değerin etrafında gerçekleşen dağılımlar için “normal dağılım”ı kullanıyoruz (Gauss dağılımı olarak da bilinir), bunu da rand yerine, randn fonksiyonunu kullanarak yapıyoruz. (normal dağılımı bütün güzellikleri ve formüler gösterimi ile birlikte “FİZ316 - İstatistik Fizik” dersinizde göreceksiniz 8):
damlalar = np.random.randn(1000,2)*4-2
plt.scatter(damlalar[:,0],damlalar[:,1],100,marker="o",alpha=0.3)
plt.show()
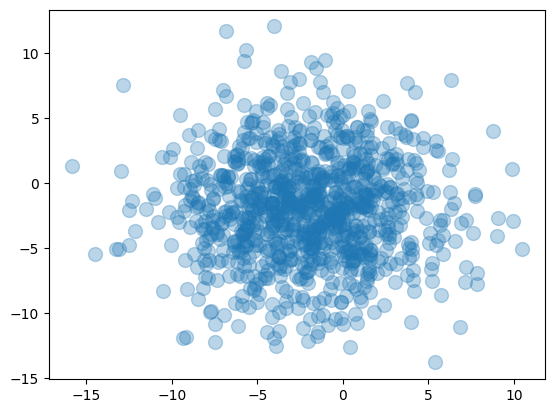
alpha parametresi ile şeffaflığı belirtiyoruz (damlalar üst üste geldikçe koyulaşıyor).
Histogram#
Histogram grafikleri dağılımları gösteren türden grafiklerdir. Örneğin, veri olarak 2022-2023 Güz Dönemi “FİZ227 - Bilgisayar Programlama” dersinin genel sınav notlarını ele alalım:
notlar = np.array([1, 1, 1, 2, 3, 3, 3, 3, 4, 4, 4,
5, 5, 5, 5, 7, 7.5, 8, 9, 11, 11,
12, 14, 16, 17, 18, 18, 20.5, 23.5,
25, 25.5, 25.5, 30, 30, 30, 30.5,
31, 35, 35, 35, 37.5, 40, 41, 43,
43, 43.5, 45, 47.5, 50, 50, 52.5,
53, 55, 55, 66, 66, 70, 70, 72.5,
77.5, 80, 90, 90, 93.5, 97.5, 100]);
Toplam 66 kişi sınava girmiş, notların dağılımını görmek için yazmamız gereken komut çok basit:
plt.hist(notlar)
plt.show()
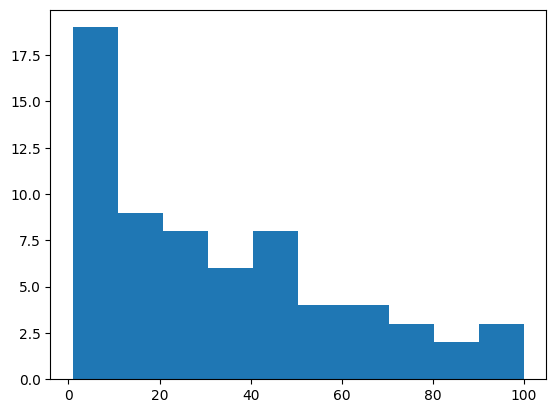
Birazcık daha anlaşılır kılalım:
plt.hist(notlar)
plt.xticks(np.arange(0,101,10))
plt.yticks(np.arange(0,21))
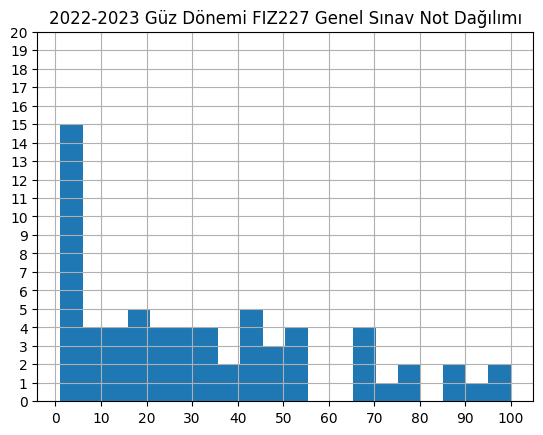
plt.title("2022-2023 Güz Dönemi FIZ227 Genel Sınav Not Dağılımı")
plt.grid(True)
plt.show()
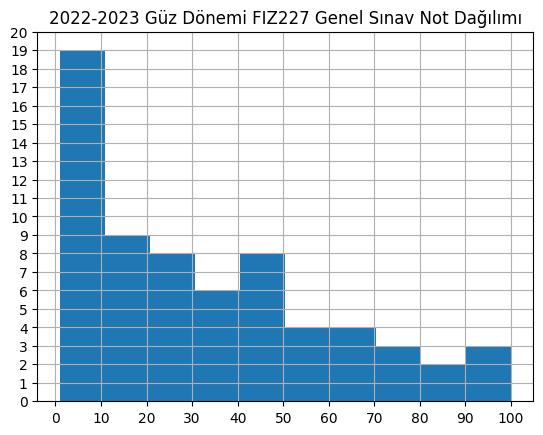
Grafiğe bakarak kolayca (0,10] aralığında 19 not olduğunu, (10,20] arasında 9 not olduğunu, vs. görebiliyoruz, ki zaten histogramın amacı da budur.
hist fonksiyonu varayılan olarak, verileri 10 kutuda toplar. İkinci bir paremetre ile kutu sayısını da belirleyebiliriz:
plt.hist(notlar,20)
plt.xticks(np.arange(0,101,10))
plt.yticks(np.arange(0,21))
plt.title("2022-2023 Güz Dönemi FIZ227 Genel Sınav Not Dağılımı")
plt.grid(True)
plt.show()
3 Boyutlu Çizimler#
Nihayet en süper görünen çizimlere gelebildik! Ama işin kod kısmına geçmeden önce, 3 boyutlu çizimin ne anlama geldiğini tartışalım biraz. 3 boyutlu çizimlerde, \(f(x,y,z)\) gibi 3 parametreli fonksiyonların grafikleri çizilmez (o 4 boyutlu bir uzay gerektiriyor maalesef), \(f(x,y)\) gibi 2 parametreli fonksiyonların grafikleri çizilir.
Kareli bir kağıt alıp, kesişim noktalarına pozitif veya negatif, çeşitli değerler yazdığınızı düşünün. Sonrasında her noktayı üzerinde yazan değer kadar pozitifse yukarı kaldırdığınızı, negatifse aşağı çektiğinizi varsayın – işte 3 boyutlu grafik böyle bir şey.
Örneğin, 2x2’lik bir matrisin 9 köşesini aşağıdaki gibi işaretlediğimizi (indislediğimizi) düşünelim:
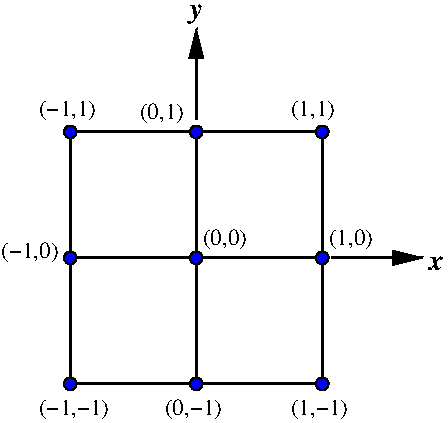
(Köşelerin koordinatlarını (indislerini) iyice inceleyin, aklınıza yatsın)
Şimdi de, her bir köşenin “z” değerini koordinatlarının karesinin toplamı olarak yazalım. Örneğin (0,-1) noktasının değeri: \(0^2+(-1)^2 = 1\) olur. Her köşenin yanına bu değerleri de yazalım:
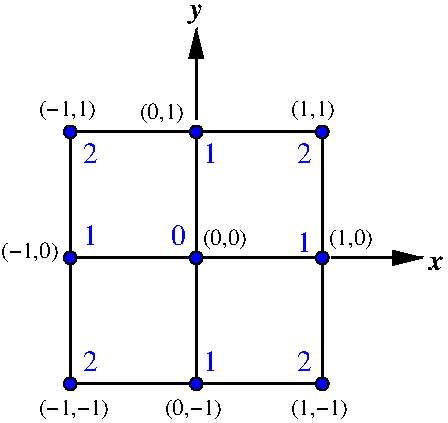
3 boyutlu grafik çizerken de tam olarak benzer bir süreçten geçiyoruz. Öncelikle, \(x=\{-1,0,1\}\) değerleri ile \(y=\{-1,0,1\}\) değerlerini harmanlayıp, (-1,-1)’den (1,1)’e olası 9 kombinasyonu üreteceğiz, sonrasında da bu koordinatlara karşılık gelen değer olarak indislerin karelerin toplamını atayacağız.
Önce harmanlama işini yapalım, bunu meshgrid() fonksiyonu ile gerçekleştiriyoruz:
tx = np.linspace(-1,1,3)
ty = np.linspace(-1,1,3)
[xx,yy] = np.meshgrid(tx,ty)
xx
array([[-1., 0., 1.],
[-1., 0., 1.],
[-1., 0., 1.]])
yy
array([[-1., -1., -1.],
[ 0., 0., 0.],
[ 1., 1., 1.]])
zz = xx**2 + yy**2
zz
array([[2., 1., 2.],
[1., 0., 1.],
[2., 1., 2.]])
from matplotlib import cm # Renk için
tx = np.linspace(-1,1,30)
ty = np.linspace(-1,1,30)
[xx,yy] = np.meshgrid(tx,ty)
zz = xx**2 + yy**2
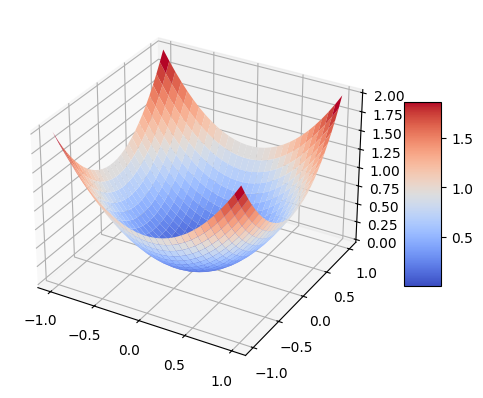
fig,ax = plt.subplots(subplot_kw={"projection": "3d"})
surf = ax.plot_surface(xx, yy, zz, cmap=cm.coolwarm,
linewidth=5)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
Renk Paletleri:
https://matplotlib.org/stable/tutorials/colors/colormaps.html
