Optimization, Minimization & Fitting Notes & Recipes

import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt

np.random.seed(371)

def g(x,mu,sigma):
    return -np.exp(-(x-mu)**2/(2*sigma**2))

x = np.linspace(0,15,100)
mu = 5
sigma = 1
plt.plot(x,g(x,mu,sigma))
plt.show()

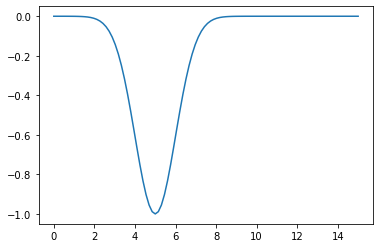
optimize.minimize(g,x0=2,args=(mu,sigma))

      fun: -1.0
 hess_inv: array([[1.00023666]])
      jac: array([0.])
  message: 'Optimization terminated successfully.'
     nfev: 24
      nit: 3
     njev: 12
   status: 0
  success: True
        x: array([5.])

Gradient Descent Algorithm

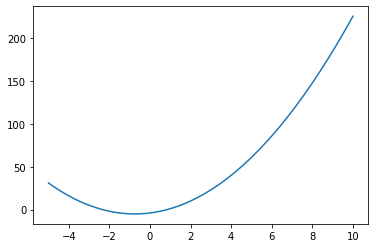
Parabol

def f(x,abc):
    return abc[0]*x**2+abc[1]*x+abc[2]
def g(x,abc):
    # Derivative
    return 2*abc[0]*x+abc[1]

xx = np.linspace(-5,10,100)
abc = np.array([2,3,-4])
plt.plot(xx,f(xx,abc))
plt.show()

x = 5
N = 50
eta = .4
tolerance = 1E-4
xs_so_far = [x]
fs_so_far = [f(x,abc)]
for i in range(N):
    gg = g(x,abc)
    print("Step #{:d}".format(i+1))
    print("The derivative (gradient) at x = {:7.5f} is {:5.3f}"\
          .format(x,gg))
    if(np.abs(gg)<tolerance):
        print("\tAs it is sufficiently close to zero, we have found the minima!")
        break
    elif(gg>0):
        print("\tAs it is positive, go left by: "+
              "(this amount)*eta(={:.2f}).".format(eta))
    else:
        print("\tAs it is negative, go right by: "+
              "|this amount|*eta(={:.2f}).".format(eta))

    delta = -gg*eta
    x0 = x
    x = x + delta
    xs_so_far.append(x)
    fs_so_far.append(f(x,abc))
    print("\t==> The new x is {:7.5f}{:+7.5f}={:7.5f}".format(x0,delta,x))
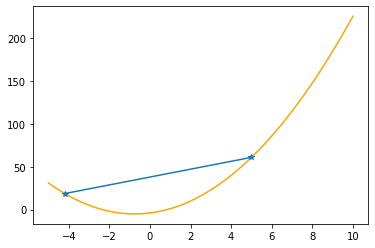
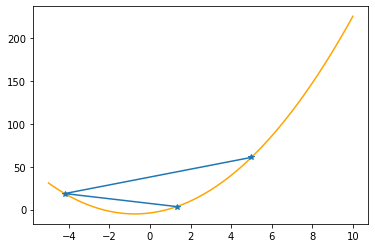
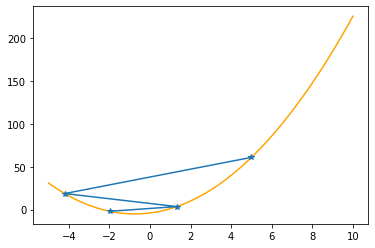
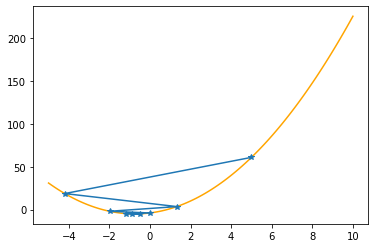
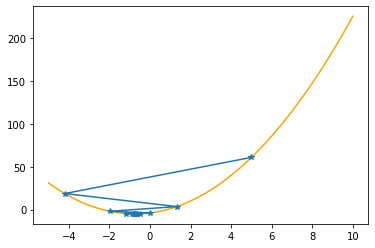
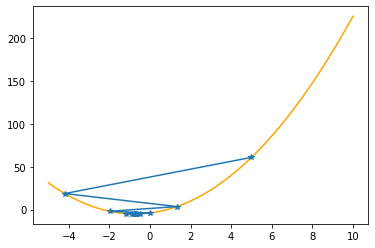
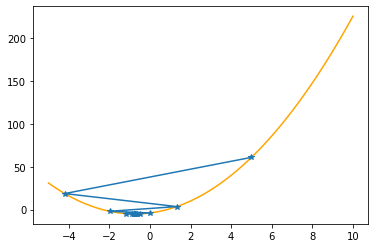
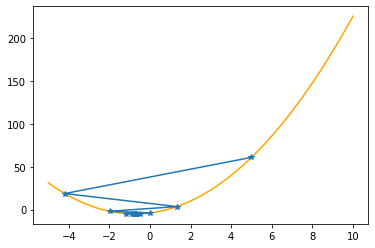
    plt.plot(xx,f(xx,abc),color="orange")
    plt.plot(xs_so_far,fs_so_far,"*-")
    plt.show()

    print("-"*45)

Step #1
The derivative (gradient) at x = 5.00000 is 23.000
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00000-9.20000=-4.20000

---------------------------------------------
Step #2
The derivative (gradient) at x = -4.20000 is -13.800
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -4.20000+5.52000=1.32000

---------------------------------------------
Step #3
The derivative (gradient) at x = 1.32000 is 8.280
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 1.32000-3.31200=-1.99200

---------------------------------------------
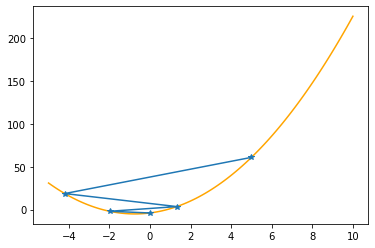
Step #4
The derivative (gradient) at x = -1.99200 is -4.968
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -1.99200+1.98720=-0.00480

---------------------------------------------
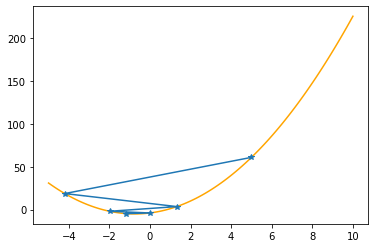
Step #5
The derivative (gradient) at x = -0.00480 is 2.981
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.00480-1.19232=-1.19712

---------------------------------------------
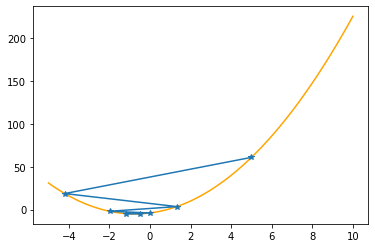
Step #6
The derivative (gradient) at x = -1.19712 is -1.788
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -1.19712+0.71539=-0.48173

---------------------------------------------
Step #7
The derivative (gradient) at x = -0.48173 is 1.073
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.48173-0.42924=-0.91096

---------------------------------------------
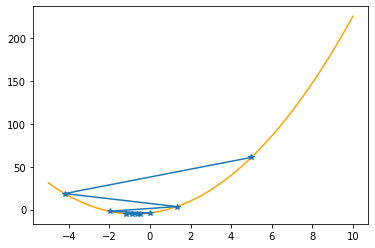
Step #8
The derivative (gradient) at x = -0.91096 is -0.644
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.91096+0.25754=-0.65342

---------------------------------------------
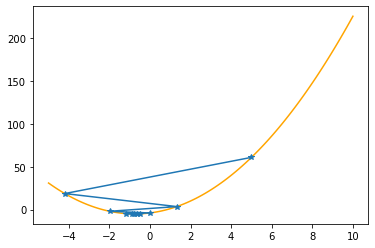
Step #9
The derivative (gradient) at x = -0.65342 is 0.386
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.65342-0.15452=-0.80795

---------------------------------------------
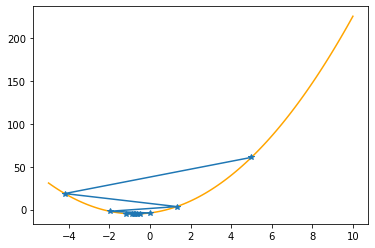
Step #10
The derivative (gradient) at x = -0.80795 is -0.232
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.80795+0.09271=-0.71523

---------------------------------------------
Step #11
The derivative (gradient) at x = -0.71523 is 0.139
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.71523-0.05563=-0.77086

---------------------------------------------
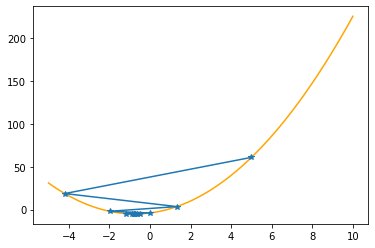
Step #12
The derivative (gradient) at x = -0.77086 is -0.083
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.77086+0.03338=-0.73748

---------------------------------------------
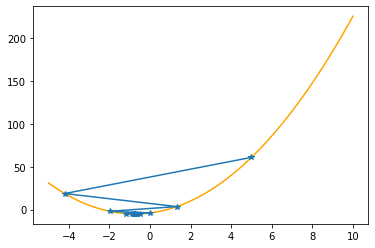
Step #13
The derivative (gradient) at x = -0.73748 is 0.050
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.73748-0.02003=-0.75751

---------------------------------------------
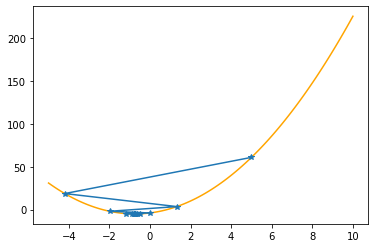
Step #14
The derivative (gradient) at x = -0.75751 is -0.030
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.75751+0.01202=-0.74549

---------------------------------------------
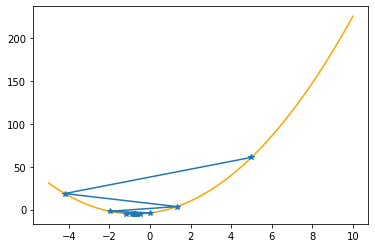
Step #15
The derivative (gradient) at x = -0.74549 is 0.018
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.74549-0.00721=-0.75270

---------------------------------------------
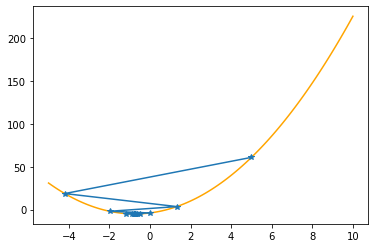
Step #16
The derivative (gradient) at x = -0.75270 is -0.011
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.75270+0.00433=-0.74838

---------------------------------------------
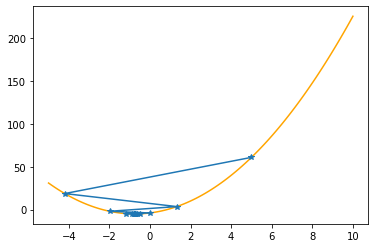
Step #17
The derivative (gradient) at x = -0.74838 is 0.006
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.74838-0.00260=-0.75097

---------------------------------------------
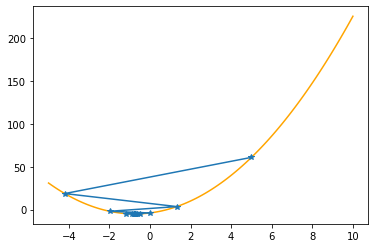
Step #18
The derivative (gradient) at x = -0.75097 is -0.004
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.75097+0.00156=-0.74942

---------------------------------------------
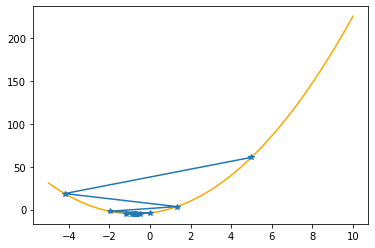
Step #19
The derivative (gradient) at x = -0.74942 is 0.002
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.74942-0.00093=-0.75035

---------------------------------------------
Step #20
The derivative (gradient) at x = -0.75035 is -0.001
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.75035+0.00056=-0.74979

---------------------------------------------
Step #21
The derivative (gradient) at x = -0.74979 is 0.001
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.74979-0.00034=-0.75013

---------------------------------------------
Step #22
The derivative (gradient) at x = -0.75013 is -0.001
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.75013+0.00020=-0.74992

---------------------------------------------
Step #23
The derivative (gradient) at x = -0.74992 is 0.000
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.74992-0.00012=-0.75005

---------------------------------------------
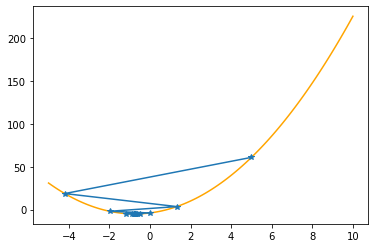
Step #24
The derivative (gradient) at x = -0.75005 is -0.000
	As it is negative, go right by: |this amount|*eta(=0.40).
	==> The new x is -0.75005+0.00007=-0.74997

---------------------------------------------
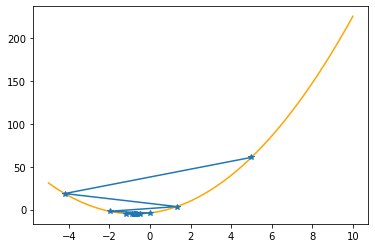
Step #25
The derivative (gradient) at x = -0.74997 is 0.000
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is -0.74997-0.00004=-0.75002

---------------------------------------------
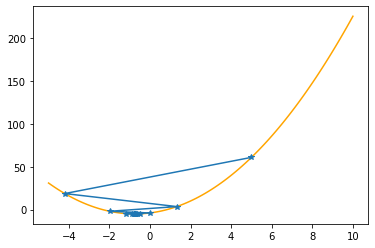
Step #26
The derivative (gradient) at x = -0.75002 is -0.000
	As it is sufficiently close to zero, we have found the minima!

# Real minimum:
np.roots([2*abc[0],abc[1]]) # root of 2ax + b

array([-0.75])

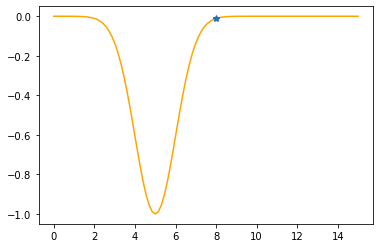
“Negative” Gaussian

def f(x,mu,sigma):
    return -np.exp(-(x-mu)**2/(2*sigma**2))
def g(x,mu,sigma):
    return (x-mu)/(sigma**2)*np.exp(-(x-mu)**2/(2*sigma**2))

mu = 5
sigma = 1

xx = np.linspace(0,15,100)
plt.plot(xx,f(xx,mu,sigma))
plt.show()

x = 8
N = 60
eta = .4
tolerance = 1E-4
xs_so_far = [x]
fs_so_far = [f(x,mu,sigma)]
for i in range(N):
    gg = g(x,mu,sigma)
    print("Step #{:d}".format(i+1))
    print("The derivative (gradient) at x = {:7.5f} is {:5.4f}"\
          .format(x,gg))
    if(np.abs(gg)<tolerance):
        print("\tAs it is sufficiently close to zero, we have found the minima!")
        break
    elif(gg>0):
        print("\tAs it is positive, go left by: "+
              "(this amount)*eta(={:.2f}).".format(eta))
    else:
        print("\tAs it is negative, go right by: "+
              "|this amount|*eta(={:.2f}).".format(eta))

    delta = -gg*eta
    x0 = x
    x = x + delta
    xs_so_far.append(x)
    fs_so_far.append(f(x,mu,sigma))
    print("\t==> The new x is {:7.5f}{:+7.5f}={:7.5f}".format(x0,delta,x))
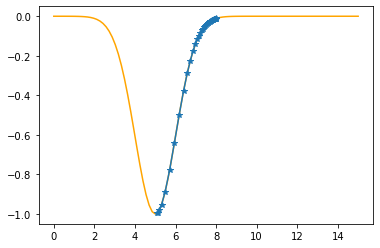
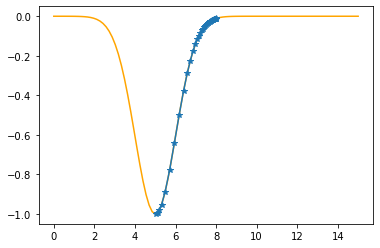
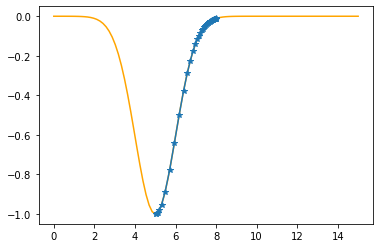
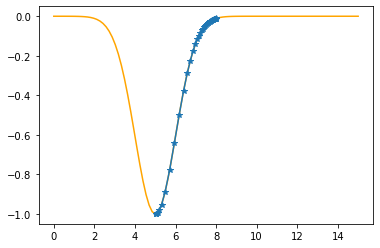
    plt.plot(xx,f(xx,mu,sigma),color="orange")
    plt.plot(xs_so_far,fs_so_far,"*-")
    plt.show()

    print("-"*45)

Step #1
The derivative (gradient) at x = 8.00000 is 0.0333
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 8.00000-0.01333=7.98667

---------------------------------------------
Step #2
The derivative (gradient) at x = 7.98667 is 0.0345
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.98667-0.01381=7.97286

---------------------------------------------
Step #3
The derivative (gradient) at x = 7.97286 is 0.0358
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.97286-0.01433=7.95853

---------------------------------------------
Step #4
The derivative (gradient) at x = 7.95853 is 0.0372
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.95853-0.01488=7.94366

---------------------------------------------
Step #5
The derivative (gradient) at x = 7.94366 is 0.0387
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.94366-0.01546=7.92819

---------------------------------------------
Step #6
The derivative (gradient) at x = 7.92819 is 0.0402
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.92819-0.01610=7.91209

---------------------------------------------
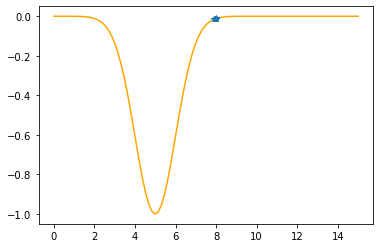
Step #7
The derivative (gradient) at x = 7.91209 is 0.0420
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.91209-0.01678=7.89531

---------------------------------------------
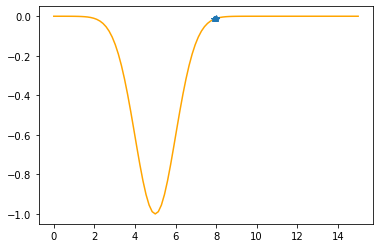
Step #8
The derivative (gradient) at x = 7.89531 is 0.0438
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.89531-0.01752=7.87780

---------------------------------------------
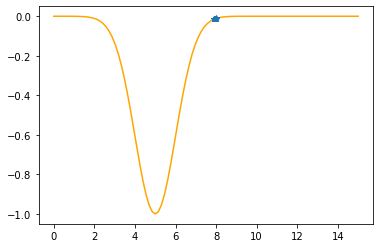
Step #9
The derivative (gradient) at x = 7.87780 is 0.0458
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.87780-0.01831=7.85948

---------------------------------------------
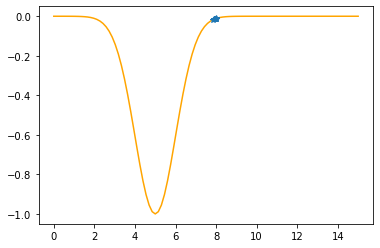
Step #10
The derivative (gradient) at x = 7.85948 is 0.0479
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.85948-0.01918=7.84031

---------------------------------------------
Step #11
The derivative (gradient) at x = 7.84031 is 0.0503
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.84031-0.02012=7.82019

---------------------------------------------
Step #12
The derivative (gradient) at x = 7.82019 is 0.0529
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.82019-0.02115=7.79904

---------------------------------------------
Step #13
The derivative (gradient) at x = 7.79904 is 0.0557
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.79904-0.02227=7.77676

---------------------------------------------
Step #14
The derivative (gradient) at x = 7.77676 is 0.0588
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.77676-0.02351=7.75325

---------------------------------------------
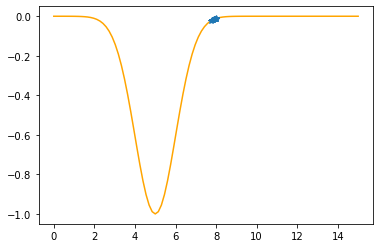
Step #15
The derivative (gradient) at x = 7.75325 is 0.0622
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.75325-0.02488=7.72837

---------------------------------------------
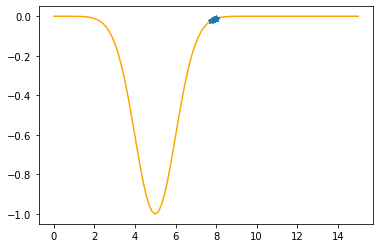
Step #16
The derivative (gradient) at x = 7.72837 is 0.0660
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.72837-0.02639=7.70198

---------------------------------------------
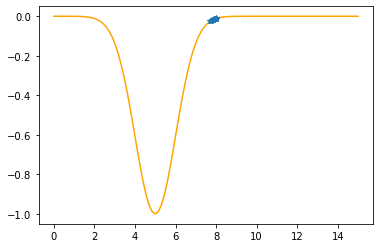
Step #17
The derivative (gradient) at x = 7.70198 is 0.0702
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.70198-0.02808=7.67389

---------------------------------------------
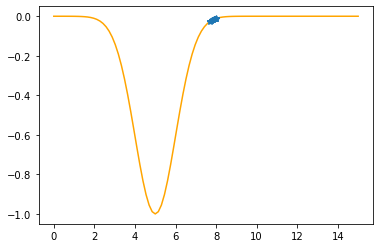
Step #18
The derivative (gradient) at x = 7.67389 is 0.0749
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.67389-0.02997=7.64393

---------------------------------------------
Step #19
The derivative (gradient) at x = 7.64393 is 0.0802
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.64393-0.03209=7.61184

---------------------------------------------
Step #20
The derivative (gradient) at x = 7.61184 is 0.0862
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.61184-0.03449=7.57735

---------------------------------------------
Step #21
The derivative (gradient) at x = 7.57735 is 0.0931
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.57735-0.03722=7.54012

---------------------------------------------
Step #22
The derivative (gradient) at x = 7.54012 is 0.1009
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.54012-0.04035=7.49978

---------------------------------------------
Step #23
The derivative (gradient) at x = 7.49978 is 0.1099
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.49978-0.04396=7.45582

---------------------------------------------
Step #24
The derivative (gradient) at x = 7.45582 is 0.1204
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.45582-0.04815=7.40766

---------------------------------------------
Step #25
The derivative (gradient) at x = 7.40766 is 0.1327
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.40766-0.05307=7.35459

---------------------------------------------
Step #26
The derivative (gradient) at x = 7.35459 is 0.1472
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.35459-0.05890=7.29569

---------------------------------------------
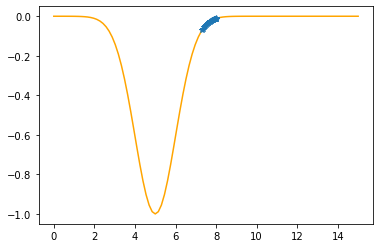
Step #27
The derivative (gradient) at x = 7.29569 is 0.1646
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.29569-0.06585=7.22984

---------------------------------------------
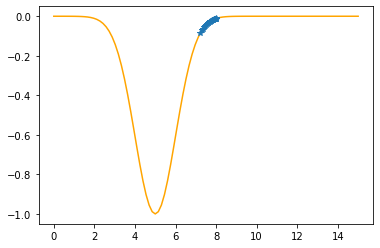
Step #28
The derivative (gradient) at x = 7.22984 is 0.1856
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.22984-0.07424=7.15560

---------------------------------------------
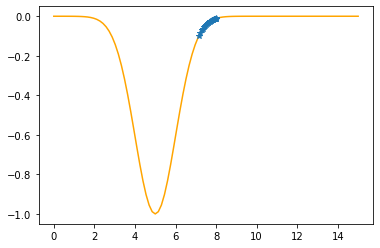
Step #29
The derivative (gradient) at x = 7.15560 is 0.2111
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.15560-0.08446=7.07115

---------------------------------------------
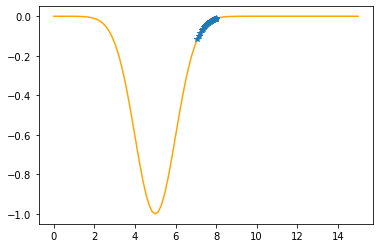
Step #30
The derivative (gradient) at x = 7.07115 is 0.2425
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 7.07115-0.09700=6.97414

---------------------------------------------
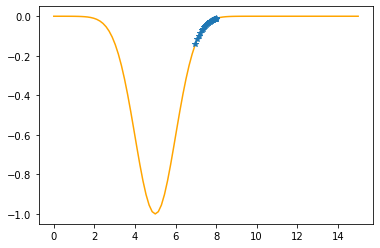
Step #31
The derivative (gradient) at x = 6.97414 is 0.2813
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 6.97414-0.11250=6.86164

---------------------------------------------
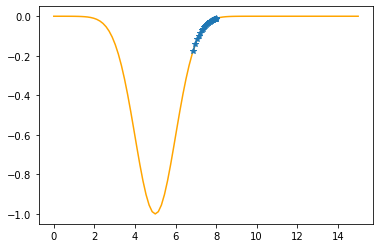
Step #32
The derivative (gradient) at x = 6.86164 is 0.3291
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 6.86164-0.13164=6.73000

---------------------------------------------
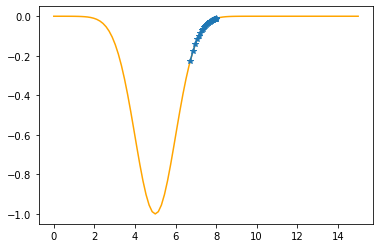
Step #33
The derivative (gradient) at x = 6.73000 is 0.3874
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 6.73000-0.15495=6.57505

---------------------------------------------
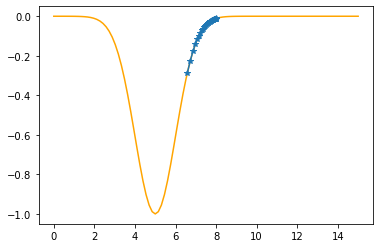
Step #34
The derivative (gradient) at x = 6.57505 is 0.4556
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 6.57505-0.18225=6.39280

---------------------------------------------
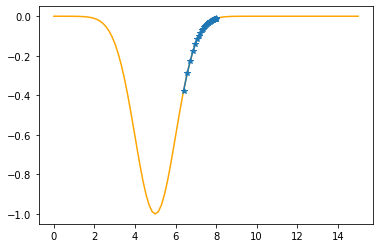
Step #35
The derivative (gradient) at x = 6.39280 is 0.5280
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 6.39280-0.21121=6.18159

---------------------------------------------
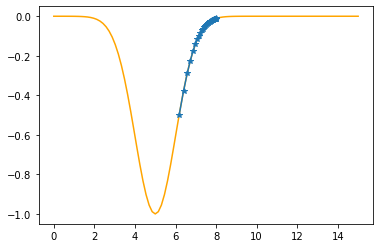
Step #36
The derivative (gradient) at x = 6.18159 is 0.5879
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 6.18159-0.23516=5.94644

---------------------------------------------
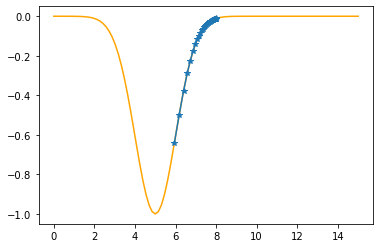
Step #37
The derivative (gradient) at x = 5.94644 is 0.6048
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.94644-0.24190=5.70453

---------------------------------------------
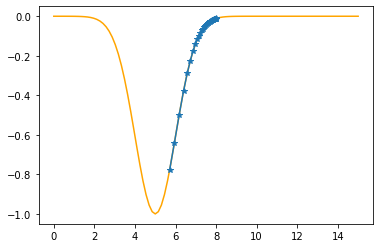
Step #38
The derivative (gradient) at x = 5.70453 is 0.5497
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.70453-0.21988=5.48466

---------------------------------------------
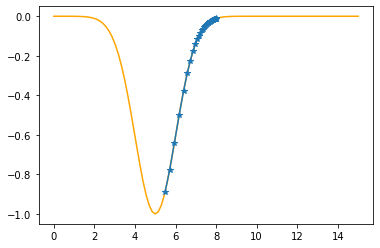
Step #39
The derivative (gradient) at x = 5.48466 is 0.4310
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.48466-0.17238=5.31228

---------------------------------------------
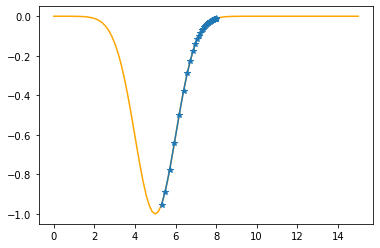
Step #40
The derivative (gradient) at x = 5.31228 is 0.2974
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.31228-0.11897=5.19331

---------------------------------------------
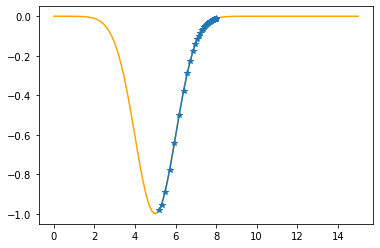
Step #41
The derivative (gradient) at x = 5.19331 is 0.1897
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.19331-0.07589=5.11742

---------------------------------------------
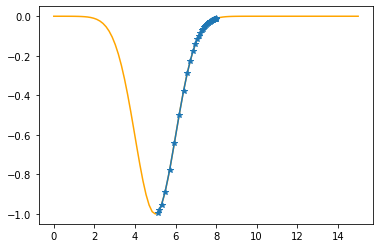
Step #42
The derivative (gradient) at x = 5.11742 is 0.1166
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.11742-0.04664=5.07077

---------------------------------------------
Step #43
The derivative (gradient) at x = 5.07077 is 0.0706
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.07077-0.02824=5.04253

---------------------------------------------
Step #44
The derivative (gradient) at x = 5.04253 is 0.0425
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.04253-0.01700=5.02554

---------------------------------------------
Step #45
The derivative (gradient) at x = 5.02554 is 0.0255
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.02554-0.01021=5.01533

---------------------------------------------
Step #46
The derivative (gradient) at x = 5.01533 is 0.0153
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.01533-0.00613=5.00920

---------------------------------------------
Step #47
The derivative (gradient) at x = 5.00920 is 0.0092
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00920-0.00368=5.00552

---------------------------------------------
Step #48
The derivative (gradient) at x = 5.00552 is 0.0055
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00552-0.00221=5.00331

---------------------------------------------
Step #49
The derivative (gradient) at x = 5.00331 is 0.0033
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00331-0.00132=5.00199

---------------------------------------------
Step #50
The derivative (gradient) at x = 5.00199 is 0.0020
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00199-0.00079=5.00119

---------------------------------------------
Step #51
The derivative (gradient) at x = 5.00119 is 0.0012
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00119-0.00048=5.00072

---------------------------------------------
Step #52
The derivative (gradient) at x = 5.00072 is 0.0007
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00072-0.00029=5.00043

---------------------------------------------
Step #53
The derivative (gradient) at x = 5.00043 is 0.0004
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00043-0.00017=5.00026

---------------------------------------------
Step #54
The derivative (gradient) at x = 5.00026 is 0.0003
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00026-0.00010=5.00015

---------------------------------------------
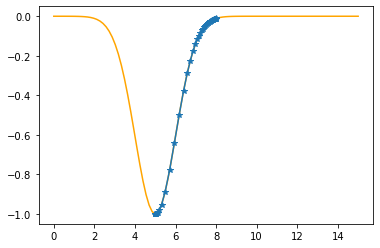
Step #55
The derivative (gradient) at x = 5.00015 is 0.0002
	As it is positive, go left by: (this amount)*eta(=0.40).
	==> The new x is 5.00015-0.00006=5.00009

---------------------------------------------
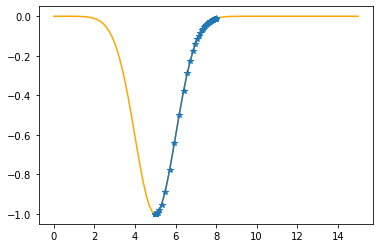
Step #56
The derivative (gradient) at x = 5.00009 is 0.0001
	As it is sufficiently close to zero, we have found the minima!

Fitting parameters via gradient descent algorithm

mu = 5
sigma = 1

N = 10
x = np.random.rand(N)*4+3
t = f(x,mu,sigma)

xx = np.linspace(3,7,100)

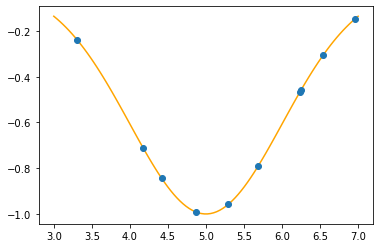
plt.plot(xx,f(xx,mu,sigma),color="orange")
plt.plot(x,t,"o")
plt.show()

\(\newcommand{\diff}{\text{d}} \newcommand{\dydx}[2]{\frac{\text{d}#1}{\text{d}#2}} \newcommand{\ddydx}[2]{\frac{\text{d}^2#1}{\text{d}#2^2}} \newcommand{\pypx}[2]{\frac{\partial#1}{\partial#2}} \newcommand{\unit}[1]{\,\text{#1}}\)

We have the data points, we know the function but we don’t have the mu & sigma.

\[f(x;\mu,\sigma)=-\exp{\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]}\]

The function we are going to try to minimize will be the difference between the real values (\(\{t_i\}\)) corresponding to \(\{x_i\}\) and the projected values (\(\{y_i\}\)):

\[F(x_i,t_i,\mu,\sigma) = t_i - f(x_i;\mu,\sigma)\]

Begin by calculating the derivatives:

\[\begin{split}\pypx{F}{\mu}=\frac{x_i-\mu}{\sigma^2}\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}\\ \pypx{F}{\sigma}=\frac{(x_i-\mu)^2}{\sigma^3}\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}\end{split}\]

(don’t forget that \(\{x_i\}\) and \(\{t_i\}\) are fixed!)

Can you see the problem in this approach? As \(\{t_i\}\) are fixed, the problem is reduced to finding the \((\mu,\sigma)\) set that will make \(f(x_i;\mu,\sigma)\) minimum, regardless of \(\{t_i\}\) values. If we follow this approach, we will end up with \((\mu,\sigma)\) that will most likely fix the values all very close to 0.

You are invited to try this approach, i.e.,

def F_mu(x,mu,sigma):
    return (x-mu)/sigma**2*np.exp(-(x-mu)**2/(2*sigma**2))
def F_sigma(x,mu,sigma):
    return (x-mu)**2/sigma**3*np.exp(-(x-mu)**2/(2*sigma**2))

But what we really have in mind is the fact that, for a given \(x_i\), we want to find values as close to the corresponding \(t_i\) as possible. One way to obtain this would be to define the error function as:

\[F(x_i,t_i,\mu,\sigma) = \left[t_i - f(x_i;\mu,\sigma)\right]^2=\left\{t_i - \left[-\exp{\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)}\right] \right\}^2\]

and then we would have the following derivatives:

\[\begin{split}\pypx{F}{\mu} = \frac{2(x_i-\mu)}{\sigma^2}\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}\left\{t_i+\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}\right\}\\ \pypx{F}{\sigma}=\frac{2(x_i-\mu)^2}{\sigma^3}\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}\left\{t_i+\exp{\left[-\frac{(x_i-\mu)^2}{2\sigma^2}\right]}\right\}\end{split}\]

(Evaluated via WolframAlpha: 1, 2)

def F_mu(x,t,mu,sigma):
    return 2*(x-mu)/sigma**2*np.exp(-(x-mu)**2/(2*sigma**2))*\
(t+np.exp(-(x-mu)**2/(2*sigma**2)))
def F_sigma(x,t,mu,sigma):
    return 2*(x-mu)**2/sigma**3*np.exp(-(x-mu)**2/(2*sigma**2))*\
(t+np.exp(-(x-mu)**2/(2*sigma**2)))

np.array([x,t]).T

array([[ 5.68303007, -0.79194365],
       [ 5.29078268, -0.95860394],
       [ 4.17595952, -0.71211109],
       [ 6.24959654, -0.45806428],
       [ 4.41660884, -0.84351919],
       [ 6.96423794, -0.14527666],
       [ 6.53987834, -0.30555892],
       [ 4.86294066, -0.99065134],
       [ 3.3056984 , -0.23803705],
       [ 6.23655758, -0.46554928]])

eta = 1

# Starting values
mu_opt = 2.7
sigma_opt = 2.3
tolerance = 1E-4

for i in range(10000):
    for ii in range(x.size):
        xi = x[ii]
        ti = t[ii]
        #print(xi,ti)
        F_mu_xi = F_mu(xi,ti,mu_opt,sigma_opt)
        F_sigma_xi = F_sigma(xi,ti,mu_opt,sigma_opt)
        mu_opt -= eta*F_mu_xi
        sigma_opt -= eta*F_sigma_xi
    total_absolute_error = np.sum(np.abs(t-f(x,mu_opt,sigma_opt)))
    if(total_absolute_error < tolerance):
        print(("As the sum of the absolute errors is sufficiently close to zero ({:.7f}),\n"+
              "\tbreaking the iteration at the {:d}. step!").
              format(total_absolute_error,i+1))
        break
print("mu: {:.4f}\tsigma: {:.4f}".format(mu_opt,sigma_opt))

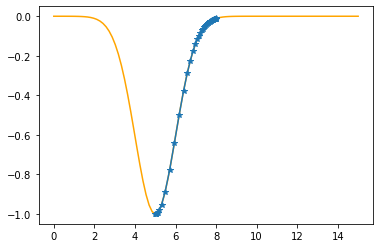
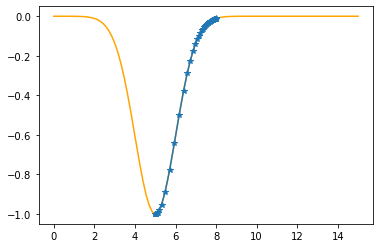
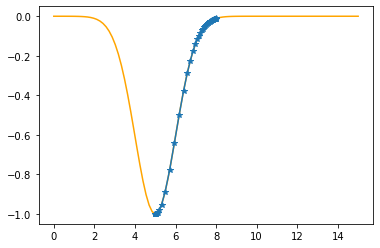
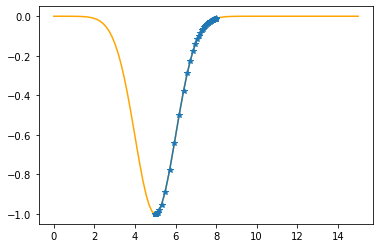
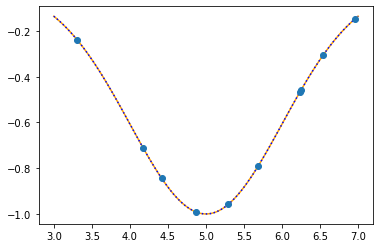
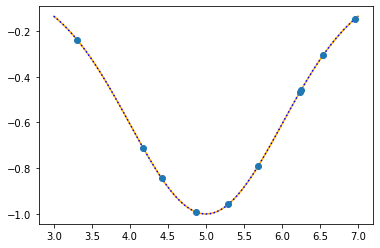
plt.plot(xx,f(xx,mu,sigma),color="orange")
plt.plot(xx,f(xx,mu_opt,sigma_opt),":b")
plt.plot(x,t,"o")
plt.show()

As the sum of the absolute errors is sufficiently close to zero (0.0000034),
	breaking the iteration at the 44. step!
mu: 5.0000	sigma: 1.0000

Stochastic Gradient Descent Algorithm

In this approach, instead of optimizing the variables at every step for one data point, we optimize them as a whole:

eta = 0.1

# Starting values
mu_opt = 2.7
sigma_opt = 2.3
tolerance = 1E-4
total_absolute_error0 = 1000

for i in range(10000):
    d_mu    = -eta*np.sum(F_mu(x,t,mu_opt,sigma_opt))
    d_sigma = -eta*np.sum(F_sigma(x,t,mu_opt,sigma_opt))

    mu_opt    += d_mu
    sigma_opt += d_sigma

    total_absolute_error = np.sum(np.abs(t-f(x,mu_opt,sigma_opt)))

    if(total_absolute_error < tolerance):
        print(("As the sum of the absolute errors is sufficiently close to zero ({:.7f}),\n"+
              "\tbreaking the iteration at the {:d}. step!").
              format(total_absolute_error,i+1))
        break
print("mu: {:.4f}\tsigma: {:.4f}".format(mu_opt,sigma_opt))

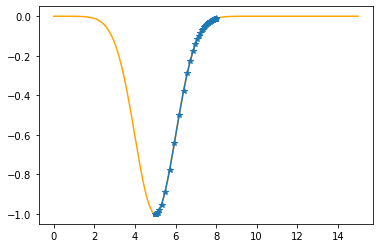
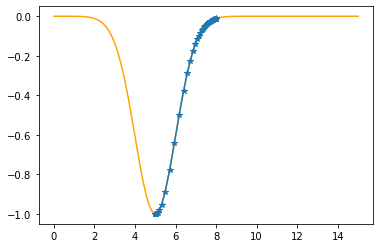
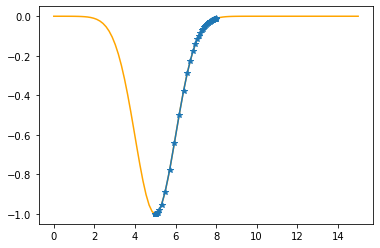
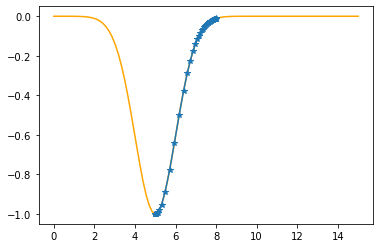
plt.plot(xx,f(xx,mu,sigma),color="orange")
plt.plot(xx,f(xx,mu_opt,sigma_opt),":b")
plt.plot(x,t,"o")
plt.show()

As the sum of the absolute errors is sufficiently close to zero (0.0000838),
	breaking the iteration at the 473. step!
mu: 5.0000	sigma: 1.0000

def F(musigma,x,t):
    return np.sum((t + np.exp(-(x-musigma[0])**2/(2*musigma[1]**2)))**2)

opt = optimize.minimize(F,x0=(2.7,2.3),args=(x,t))
opt.x,opt.fun

(array([-0.94939593,  6.24977685]), 0.7517808253037702)

opt = optimize.minimize(F,x0=(2.7,2.3),args=(x,t),bounds=[(3,6.5),(None,None)])
opt.x,opt.fun

(array([5.00000008, 0.99999998]), 1.0592809689731542e-14)