Information Theory Application#
FIZ371 - Scientific & Technical Computations | 01/05/2020
Information Theory Application
Message Transmission Over A Noisy Channel
Original Message (Smiley Image)
Adding noise
Repetition Algorithm
Encoding the message before transmission over the noisy channel and decoding it on the otherside
With 3-repetition:
With 5-repetition:
Hamming Code (7,4)
Encoding the message before transmission over the noisy channel and decoding it on the otherside
Dr. Emre S. Tasci emre.tasci@hacettepe.edu.tr
Message Transmission Over A Noisy Channel#
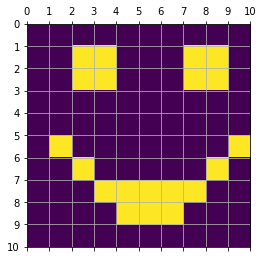
Original Message (Smiley Image)#
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(371)
smiley = np.zeros([10,10])
smiley[1,[2,3,7,8]] = 1
smiley[2,[2,3,7,8]] = 1
smiley[5,[1,9]] = 1
smiley[6,[2,8]] = 1
smiley[7,3:8] = 1
smiley[8,4:7] = 1
print(smiley)
def show_mat(mat):
plt.matshow(mat);
plt.xticks(np.arange(-0.5,mat.shape[1]),np.arange(0,mat.shape[1]+1))
plt.yticks(np.arange(-0.5,mat.shape[0]),np.arange(0,mat.shape[0]+1))
plt.grid(True)
plt.show()
show_mat(smiley)
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 1. 0. 0. 0. 1. 1. 0.]
[0. 0. 1. 1. 0. 0. 0. 1. 1. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 1. 0. 0. 0. 0. 0. 1. 0.]
[0. 0. 0. 1. 1. 1. 1. 1. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
aa = np.random.rand(10,10)
print(aa)
[[0.67075752 0.57269567 0.29398988 0.81239913 0.35415221 0.99105949
0.88496959 0.46573517 0.0764246 0.8091394 ]
[0.69593246 0.44876677 0.53807358 0.73339083 0.82003486 0.88569963
0.91761344 0.63732089 0.20199076 0.59188455]
[0.05436861 0.2559915 0.7163759 0.13360297 0.58648529 0.55840365
0.33722727 0.42298327 0.12892243 0.19292516]
[0.96169087 0.89508277 0.19653927 0.50537714 0.04472516 0.57391799
0.34880585 0.75404504 0.123654 0.54809687]
[0.39099071 0.88942276 0.02249352 0.22536184 0.84507417 0.32605968
0.38400221 0.21591123 0.60647952 0.95785814]
[0.57987987 0.9925049 0.28028669 0.3101683 0.04994884 0.95405887
0.30315847 0.92951376 0.06005859 0.51998037]
[0.7906905 0.54485387 0.25215364 0.79740887 0.60098187 0.92367802
0.07903193 0.52125442 0.38381823 0.81985423]
[0.32307813 0.59489293 0.75157259 0.0200778 0.02551564 0.55275974
0.26424553 0.62760059 0.88005822 0.97640319]
[0.35837069 0.44730676 0.17721113 0.58766026 0.91042897 0.44743822
0.17720952 0.13873409 0.80870951 0.12107576]
[0.88300007 0.27978674 0.99001526 0.92851086 0.97474366 0.99145558
0.11483757 0.96526171 0.2944525 0.80592827]]
np.sum(aa<0.25)
22
aa[aa<0.25] = 1
aa[aa<1] = 0
aa
array([[0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
[1., 0., 0., 1., 0., 0., 0., 0., 1., 1.],
[0., 0., 1., 0., 1., 0., 0., 0., 1., 0.],
[0., 0., 1., 1., 0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 1., 0., 0., 0., 1., 0.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 1., 1., 0., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0., 1., 1., 0., 1.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.]])
Adding noise#
def rand_filter(mat,beta):
# Flip each of the given mat's cells with
# a probability of beta
size = mat.shape
rnd = (np.random.rand(size[0],size[1])<beta).astype(int)
res = np.logical_xor(mat,rnd).astype(int)
#print(rnd)
print(res)
#show_mat(res)
print("# Flipped cells: %2d"%(np.sum(rnd)))
print("Ratio of the flipped cells to total: %.3f"%(np.sum(rnd)/mat.size))
return res
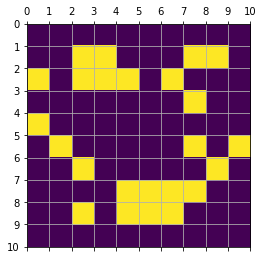
smiley_with_noise = rand_filter(smiley,0.1)
show_mat(smiley_with_noise)
[[0 0 0 0 0 0 0 0 0 0]
[0 0 1 1 0 0 0 1 1 0]
[1 0 1 1 1 0 1 0 0 0]
[0 0 0 0 0 0 0 1 0 0]
[1 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 1 0 1]
[0 0 1 0 0 0 0 0 1 0]
[0 0 0 0 1 1 1 1 0 0]
[0 0 1 0 1 1 1 0 0 0]
[0 0 0 0 0 0 0 0 0 0]]
# Flipped cells: 10
Ratio of the flipped cells to total: 0.100
Repetition Algorithm#
def rep_enc(mat,n):
# Repeat the given mat's each cell n times
size = mat.shape
print(size)
mat_repeated = np.empty([size[0],n*size[1]])
print (mat_repeated.shape)
for i in range(size[0]):
for j in range(size[1]):
#print(i,j,":",np.arange(n*j,n*j+n),mat[i,j])
mat_repeated[i,np.arange(n*j,n*j+n)] = mat[i,j]
return mat_repeated
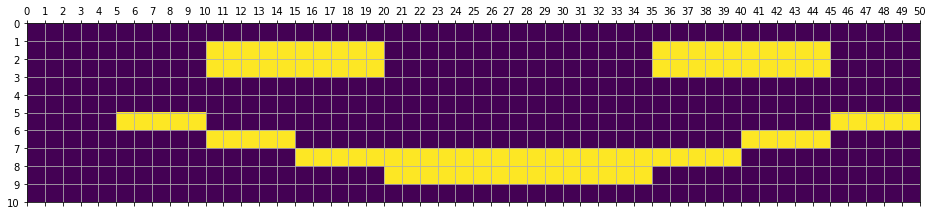
smiley_encoded = rep_enc(smiley,5)
#print(a)
show_mat(smiley_encoded)
(10, 10)
(10, 50)
def rep_dec(mat,n):
# Decodes the given mat, in accordance with
# the given repetition number n
size = mat.shape
res = np.empty([size[0],int(size[1]/n)])
res_size = res.shape
for i in range(size[0]):
for j in range(res_size[1]):
#print("%d %d"%(i,j))
res[i,j] = (np.sum(mat[i,np.arange(n*j,n*j+n)])>(n/2)).astype(int)
return res
show_mat(rep_dec(rep_enc(smiley,5),5))
(10, 10)
(10, 50)

Encoding the message before transmission over the noisy channel and decoding it on the otherside#
With 3-repetition:#
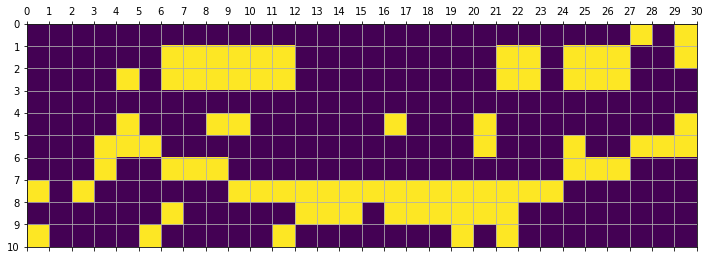
smiley_encoded = rep_enc(smiley,3)
smiley_enc_transmitted = rand_filter(smiley_encoded,0.1)
show_mat(smiley_enc_transmitted)
smiley_decoded = rep_dec(smiley_enc_transmitted,3)
print(smiley_decoded.shape)
show_mat(smiley_decoded)
# Calculate the number of flipped cells
print("# Flipped cells: %2d"%np.sum(np.logical_xor(smiley,smiley_decoded)))
print("Ratio of the flipped cells to total: %.3f"%(np.sum(np.logical_xor(smiley,smiley_decoded))/smiley.size))
(10, 10)
(10, 30)
[[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1]
[0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 0 1]
[0 0 0 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1]
[0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 1]
[0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0]
[1 0 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0]
[0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0]
[1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0]]
# Flipped cells: 25
Ratio of the flipped cells to total: 0.083
(10, 10)
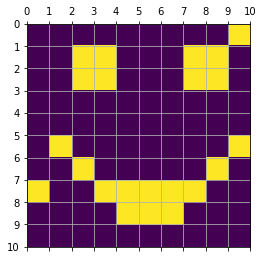
# Flipped cells: 2
Ratio of the flipped cells to total: 0.020
With 5-repetition:#
smiley_encoded = rep_enc(smiley,5)
smiley_enc_transmitted = rand_filter(smiley_encoded,0.1)
show_mat(smiley_enc_transmitted)
smiley_decoded = rep_dec(smiley_enc_transmitted,5)
print(smiley_decoded.shape)
show_mat(smiley_decoded)
# Calculate the number of flipped cells
print("# Flipped cells: %2d"%np.sum(np.logical_xor(smiley,smiley_decoded)))
print("Ratio of the flipped cells to total: %.3f"%(np.sum(np.logical_xor(smiley,smiley_decoded))/smiley.size))
(10, 10)
(10, 50)
[[0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 1 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 1 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 1
1 1 1 0 1 1 1 1 1 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 0 0 0 1 0]
[0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 1]
[0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0
1 0 0 0 0 0 1 0 0 1 1 1 1 1]
[0 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 1 1 1 1 1 0 0 1 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 1 0 0]]
# Flipped cells: 53
Ratio of the flipped cells to total: 0.106
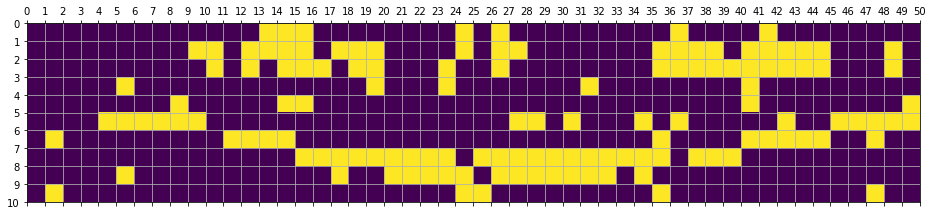
(10, 10)

# Flipped cells: 0
Ratio of the flipped cells to total: 0.000
Hamming Code (7,4)#
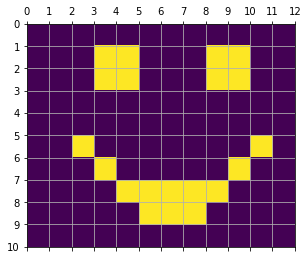
To efficiently employ the (7,4) Hamming Code, we are increasing our smiley’s dimensions to 10x12 to comply with the 4 bit packages of data (4x3=12).
smiley_12 = np.zeros([10,12])
smiley_12[:,1:11] = smiley
show_mat(smiley_12)
def H74_enc(mat):
size = mat.shape
if(size[1]%4):
print("The number of columns must be a multiple of 4!")
res = np.empty([size[0],int(size[1]/4*7)])
a = 0
for i in range(size[0]):
for j in range(int(size[1]/4)):
a += 1
current_4 = mat[i,range(4*j,4*j+4)]
print(current_4,end="")
t5 = int(np.sum(current_4[0:3])%2)
t6 = int(np.sum(current_4[1:4])%2)
t7 = int(np.sum(current_4[[0,2,3]])%2)
print(t5,t6,t7,end="|")
res[i,range(7*j,7*j+7)] = np.concatenate((current_4,[t5],[t6],[t7]))
print ("")
return res
encd_H74 = H74_enc(smiley_12)
print(encd_H74)
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 0. 1.]0 1 1|[1. 0. 0. 0.]1 0 1|[1. 1. 0. 0.]0 1 1|
[0. 0. 0. 1.]0 1 1|[1. 0. 0. 0.]1 0 1|[1. 1. 0. 0.]0 1 1|
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 1. 0.]1 1 1|[0. 0. 0. 0.]0 0 0|[0. 0. 1. 0.]1 1 1|
[0. 0. 0. 1.]0 1 1|[0. 0. 0. 0.]0 0 0|[0. 1. 0. 0.]1 1 0|
[0. 0. 0. 0.]0 0 0|[1. 1. 1. 1.]1 1 1|[1. 0. 0. 0.]1 0 1|
[0. 0. 0. 0.]0 0 0|[0. 1. 1. 1.]0 1 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 1. 1.]
[0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 1. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 1. 1. 1.]
[0. 0. 0. 1. 0. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 1. 1. 0.]
[0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0. 1. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
syndromes = np.empty([2,2,2],dtype=int)
syndromes[0,0,0] = -1
syndromes[0,0,1] = 6
syndromes[0,1,0] = 5
syndromes[0,1,1] = 3
syndromes[1,0,0] = 4
syndromes[1,0,1] = 0
syndromes[1,1,0] = 1
syndromes[1,1,1] = 2
def H74_dec(mat):
size = mat.shape
print(size)
if(size[1]%7):
print("The number of columns must be a multiple of 7!")
res = np.empty([size[0],int(size[1]/7*4)])
for i in range(size[0]):
for j in range(int(size[1]/7)):
current_7 = mat[i,range(7*j,7*j+7)]
z1 = int(np.sum(current_7[[4,0,1,2]])%2)
z2 = int(np.sum(current_7[[5,1,2,3]])%2)
z3 = int(np.sum(current_7[[6,0,2,3]])%2)
syndrome = syndromes[z1,z2,z3]
print(i,j,current_7,[z1,z2,z3]," ==> flip:","{:-2d}.bit".format(syndrome),end=" | ")
#if(syndrome>-1 and syndrome<5):
if(syndrome>-1):
current_7[syndrome] = np.logical_xor(current_7[syndrome],1)
print(current_7,end="")
res[i,range(4*j,4*j+4)] = current_7[0:4]
print("")
return(res)
# H74_dec(encd_H74)
Encoding the message before transmission over the noisy channel and decoding it on the otherside#
encd_H74 = H74_enc(smiley_12)
encd_H74_noise = rand_filter(encd_H74,0.1)
decd_H74 = H74_dec(encd_H74_noise)
show_mat(decd_H74)
# Calculate the number of flipped cells
print("# Flipped cells: %2d"%np.sum(np.logical_xor(smiley_12,decd_H74)))
print("Ratio of the flipped cells to total: %.3f"%(np.sum(np.logical_xor(smiley_12,decd_H74))/smiley_12.size))
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 0. 1.]0 1 1|[1. 0. 0. 0.]1 0 1|[1. 1. 0. 0.]0 1 1|
[0. 0. 0. 1.]0 1 1|[1. 0. 0. 0.]1 0 1|[1. 1. 0. 0.]0 1 1|
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 1. 0.]1 1 1|[0. 0. 0. 0.]0 0 0|[0. 0. 1. 0.]1 1 1|
[0. 0. 0. 1.]0 1 1|[0. 0. 0. 0.]0 0 0|[0. 1. 0. 0.]1 1 0|
[0. 0. 0. 0.]0 0 0|[1. 1. 1. 1.]1 1 1|[1. 0. 0. 0.]1 0 1|
[0. 0. 0. 0.]0 0 0|[0. 1. 1. 1.]0 1 0|[0. 0. 0. 0.]0 0 0|
[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|[0. 0. 0. 0.]0 0 0|
[[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1]
[0 0 0 1 0 1 1 1 0 0 0 1 0 1 1 1 0 1 0 1 1]
[0 0 0 0 1 0 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1]
[0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 1 0 1 1 1 1 0 0 1 0 0 0 0 0 1 1 1 1 1]
[0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 1 1 1 0]
[0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 0 0 0 1 0 1]
[0 1 0 0 1 0 0 0 1 1 1 0 1 0 0 1 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0]]
# Flipped cells: 22
Ratio of the flipped cells to total: 0.105
(10, 21)
0 0 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
0 1 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
0 2 [0 0 0 1 0 0 1] [0, 1, 0] ==> flip: 5.bit | [0 0 0 1 0 1 1]
1 0 [0 0 0 1 0 1 1] [0, 0, 0] ==> flip: -1.bit |
1 1 [1 0 0 0 1 0 1] [0, 0, 0] ==> flip: -1.bit |
1 2 [1 1 0 1 0 1 1] [0, 1, 1] ==> flip: 3.bit | [1 1 0 0 0 1 1]
2 0 [0 0 0 0 1 0 1] [1, 0, 1] ==> flip: 0.bit | [1 0 0 0 1 0 1]
2 1 [1 0 0 0 1 0 1] [0, 0, 0] ==> flip: -1.bit |
2 2 [1 1 0 0 0 1 1] [0, 0, 0] ==> flip: -1.bit |
3 0 [0 0 0 0 1 0 0] [1, 0, 0] ==> flip: 4.bit | [0 0 0 0 0 0 0]
3 1 [0 0 0 0 0 0 1] [0, 0, 1] ==> flip: 6.bit | [0 0 0 0 0 0 0]
3 2 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
4 0 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
4 1 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
4 2 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
5 0 [0 0 1 0 1 1 1] [0, 0, 0] ==> flip: -1.bit |
5 1 [1 0 0 1 0 0 0] [1, 1, 0] ==> flip: 1.bit | [1 1 0 1 0 0 0]
5 2 [0 0 1 1 1 1 1] [0, 1, 1] ==> flip: 3.bit | [0 0 1 0 1 1 1]
6 0 [0 0 0 1 0 0 0] [0, 1, 1] ==> flip: 3.bit | [0 0 0 0 0 0 0]
6 1 [0 1 0 0 0 0 0] [1, 1, 0] ==> flip: 1.bit | [0 0 0 0 0 0 0]
6 2 [1 1 0 1 1 1 0] [1, 1, 0] ==> flip: 1.bit | [1 0 0 1 1 1 0]
7 0 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
7 1 [1 1 0 1 1 1 1] [1, 1, 1] ==> flip: 2.bit | [1 1 1 1 1 1 1]
7 2 [1 0 0 0 1 0 1] [0, 0, 0] ==> flip: -1.bit |
8 0 [0 1 0 0 1 0 0] [0, 1, 0] ==> flip: 5.bit | [0 1 0 0 1 1 0]
8 1 [0 1 1 1 0 1 0] [0, 0, 0] ==> flip: -1.bit |
8 2 [0 1 0 0 0 0 0] [1, 1, 0] ==> flip: 1.bit | [0 0 0 0 0 0 0]
9 0 [0 0 0 0 0 0 0] [0, 0, 0] ==> flip: -1.bit |
9 1 [0 0 0 0 1 0 0] [1, 0, 0] ==> flip: 4.bit | [0 0 0 0 0 0 0]
9 2 [0 0 1 0 0 0 0] [1, 1, 1] ==> flip: 2.bit | [0 0 0 0 0 0 0]
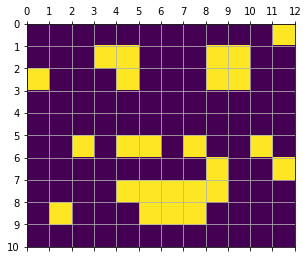
# Flipped cells: 11
Ratio of the flipped cells to total: 0.092
Homework: Develop Hamming Code (8,4), calculate its probability error, discuss why HC(7,4) is preferable to HC(8,4) – compare it with the double repetition algorithm R2.
