Final Exam

Final Exam#

FIZ371 - Scientific & Technical Calculations | 10/01/2024

Emre S. Tasci emre.tasci@hacettepe.edu.tr Eng. Physics Dept.
Hacettepe University
Ankara, Turkey

You can solve the problems analytically or stochastically, it’s up to you. You can present your solution having been calculated on a paper, or as a jupyter notebook, or as a mixture of both.

  • Please prepare one jupyter notebook per question.

  • You can use any predefined function from numpy, scipy, math, pandas, random, collections and matplotlib modules – for any other external module/library you should first ask for permission.

  • Before submitting, download your notebooks as html as well as ipynb format and zip them all.

  • Name your zip file as <YourName>_FIZ371_Final.zip (e.g., EmreTasci_FIZ371_Resit.zip)

Pick any 2 questions, if you have time go for a 3rd one for half the points (25) as bonus. Good luck! 8)

1. Probability#

A bag contains \(w\) white balls and \(b\) black balls. Two balls are drawn, one after the other, without replacement.

Prove that the probability that the first ball is white is equal to the probability that the second is white.

2. Identifying the Distribution#

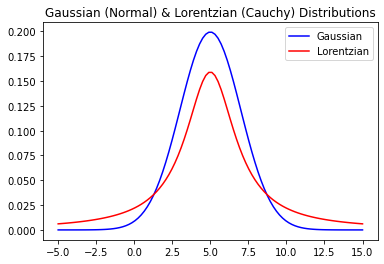
Suppose that you have been given a set of \(N\) data points and you have been told that these data are obtained from either a Gaussian distribution or a Lorentz distribution (their normalized forms are included below). How do you determine the probability that the data belongs to the Gaussian or the Lorentzian distribution? Express your answer in detail, using mathematical approach.

  • Gaussian Distribution

    \[G(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\]

  • Lorentzian Distributiton

    \[L(x;x_0,\gamma) = \frac{1}{\pi}\left[\frac{\gamma}{\left(x-x_0\right)^2+\gamma^2}\right]\]
import numpy as np
import matplotlib.pyplot as plt

def G(x,mu,sigma):
    return np.exp(-0.5*((x-mu)/sigma)**2)/(sigma*np.sqrt(2*np.pi))

def L(x,x0,gamma):
    return (gamma/np.pi)/((x-x0)**2+gamma**2)

x = np.linspace(-5,15,100)
plt.plot(x,G(x,5,2),"b-")
plt.plot(x,L(x,5,2),"r-")
plt.legend(["Gaussian","Lorentzian"])
plt.title("Gaussian (Normal) & Lorentzian (Cauchy) Distributions")
plt.show()
../_images/f08c84e80bb03eff23491959b7a227d4cbfe491dad36548eebe5414fa6e8a2f1.png

3. Game Theory#

Three candies are given to one of the two friends. The one to whom the candidates are given, will distribute them and the other will decide if it is acceptable or not. If he/she declares the deal as not acceptable, then none of them will get any candy.

Draw the reaction-correspondence graph, indicate Nash equilibrium points if there are any.

Calculate the probabilities that the decider will accept the deal (if any of the probabilities is 0 or 1 then re-construct the pay-off table, and redo the calculations!).

4. 2D Cellular Automata#

Start from the center of a \(15\times15\) grid. Come up with a set of rules to build an expanding circle out of that center. The inside of the circle can be left filled (i.e., it can be a disk instead of a circle).

5. Hexagonal Antiferromagnetic Ising Model#

(Counts as a double question)

Modify the existing code or rewrite a new one to accompany a hexagonal grid where each site is affected by its 3 nearest neighbours and each “bond” contributes either:

  • \(-|J|\) to the energy when the sites are of opposite spins, or,

  • \(|J|\) to the energy when the sites are of parallel spins

Contents