Contents

Least Squares Method & Error Estimations

Least Squares Method & Error Estimations

FIZ228 - Numerical Analysis
Dr. Emre S. Tasci, Hacettepe University

Note

This lecture is heavily benefited from Steven Chapra’s Applied Numerical Methods with MATLAB: for Engineers & Scientists.

Data & Import

The free-fall data we will be using is taken from: D. Horvat & R. Jecmenica, “The Free Fall Experiment” Resonance 21 259-275 (2016) [https://doi.org/10.1007/s12045-016-0321-9].

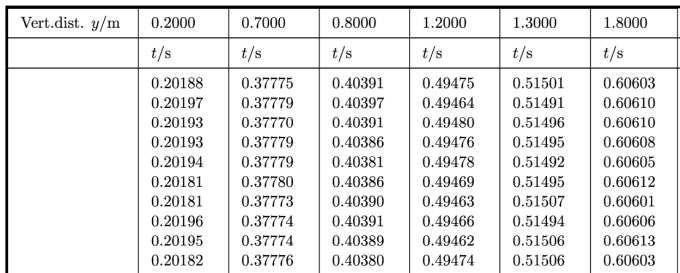
03_FreeFallData.png

Here’s the content of our data file:

Vert.dist. y/m,0.2,0.7,0.8,1.2,1.3,1.8
,t/s,t/s,t/s,t/s,t/s,t/s
1,0.20188,0.37775,0.40391,0.49475,0.51501,0.60603
2,0.20197,0.37779,0.40397,0.49464,0.51491,0.60610
3,0.20193,0.37770,0.40391,0.49480,0.51496,0.60610
4,0.20193,0.37779,0.40386,0.49476,0.51495,0.60608
5,0.20194,0.37779,0.40381,0.49478,0.51492,0.60605
6,0.20181,0.37780,0.40386,0.49469,0.51495,0.60612
7,0.20181,0.37773,0.40390,0.49463,0.51507,0.60601
8,0.20196,0.37774,0.40391,0.49466,0.51494,0.60606
9,0.20195,0.37774,0.40389,0.49462,0.51506,0.60613
10,0.20182,0.37776,0.40380,0.49474,0.51506,0.60603
<t>/s,0.20190,0.37776,0.40388,0.49471,0.51498,0.60607

03_FreeFallData.csv

import pandas as pd
data1 = pd.read_csv("data/03_FreeFallData.csv")
data1.columns
data1
Vert.dist. y/m 0.2 0.7 0.8 1.2 1.3 1.8
0 NaN t/s t/s t/s t/s t/s t/s
1 1 0.20188 0.37775 0.40391 0.49475 0.51501 0.60603
2 2 0.20197 0.37779 0.40397 0.49464 0.51491 0.60610
3 3 0.20193 0.37770 0.40391 0.49480 0.51496 0.60610
4 4 0.20193 0.37779 0.40386 0.49476 0.51495 0.60608
5 5 0.20194 0.37779 0.40381 0.49478 0.51492 0.60605
6 6 0.20181 0.37780 0.40386 0.49469 0.51495 0.60612
7 7 0.20181 0.37773 0.40390 0.49463 0.51507 0.60601
8 8 0.20196 0.37774 0.40391 0.49466 0.51494 0.60606
9 9 0.20195 0.37774 0.40389 0.49462 0.51506 0.60613
10 10 0.20182 0.37776 0.40380 0.49474 0.51506 0.60603
11 <t>/s 0.20190 0.37776 0.40388 0.49471 0.51498 0.60607

We don’t need the first row and first column, so let’s remove them via pandas.DataFrame.drop:

data1.drop(0, inplace=True)
data1.drop(11, inplace=True)
data1.drop(['Vert.dist. y/m'],axis=1, inplace=True)
data1
0.2 0.7 0.8 1.2 1.3 1.8
1 0.20188 0.37775 0.40391 0.49475 0.51501 0.60603
2 0.20197 0.37779 0.40397 0.49464 0.51491 0.60610
3 0.20193 0.37770 0.40391 0.49480 0.51496 0.60610
4 0.20193 0.37779 0.40386 0.49476 0.51495 0.60608
5 0.20194 0.37779 0.40381 0.49478 0.51492 0.60605
6 0.20181 0.37780 0.40386 0.49469 0.51495 0.60612
7 0.20181 0.37773 0.40390 0.49463 0.51507 0.60601
8 0.20196 0.37774 0.40391 0.49466 0.51494 0.60606
9 0.20195 0.37774 0.40389 0.49462 0.51506 0.60613
10 0.20182 0.37776 0.40380 0.49474 0.51506 0.60603

Be careful that the data have been imported as string (due to the first row initially being formed of strings 8P ):

data1.loc[2,"0.7"]

'0.37779'

type(data1.loc[2,"0.7"])

str

data1.dtypes

0.2    object
0.7    object
0.8    object
1.2    object
1.3    object
1.8    object
dtype: object

So, let’s set them all to float:

data1 = data1.astype('float')
data1.dtypes

0.2    float64
0.7    float64
0.8    float64
1.2    float64
1.3    float64
1.8    float64
dtype: object

data1
0.2 0.7 0.8 1.2 1.3 1.8
1 0.20188 0.37775 0.40391 0.49475 0.51501 0.60603
2 0.20197 0.37779 0.40397 0.49464 0.51491 0.60610
3 0.20193 0.37770 0.40391 0.49480 0.51496 0.60610
4 0.20193 0.37779 0.40386 0.49476 0.51495 0.60608
5 0.20194 0.37779 0.40381 0.49478 0.51492 0.60605
6 0.20181 0.37780 0.40386 0.49469 0.51495 0.60612
7 0.20181 0.37773 0.40390 0.49463 0.51507 0.60601
8 0.20196 0.37774 0.40391 0.49466 0.51494 0.60606
9 0.20195 0.37774 0.40389 0.49462 0.51506 0.60613
10 0.20182 0.37776 0.40380 0.49474 0.51506 0.60603

While we’re at it, let’s do a couple of make-overs:

data1.reset_index(inplace=True,drop=True)
data1
0.2 0.7 0.8 1.2 1.3 1.8
0 0.20188 0.37775 0.40391 0.49475 0.51501 0.60603
1 0.20197 0.37779 0.40397 0.49464 0.51491 0.60610
2 0.20193 0.37770 0.40391 0.49480 0.51496 0.60610
3 0.20193 0.37779 0.40386 0.49476 0.51495 0.60608
4 0.20194 0.37779 0.40381 0.49478 0.51492 0.60605
5 0.20181 0.37780 0.40386 0.49469 0.51495 0.60612
6 0.20181 0.37773 0.40390 0.49463 0.51507 0.60601
7 0.20196 0.37774 0.40391 0.49466 0.51494 0.60606
8 0.20195 0.37774 0.40389 0.49462 0.51506 0.60613
9 0.20182 0.37776 0.40380 0.49474 0.51506 0.60603

Plotting

import seaborn as sns
sns.set_theme() # To make things appear "more beautiful" 8)

data2 = data1.copy()
data2
0.2 0.7 0.8 1.2 1.3 1.8
0 0.20188 0.37775 0.40391 0.49475 0.51501 0.60603
1 0.20197 0.37779 0.40397 0.49464 0.51491 0.60610
2 0.20193 0.37770 0.40391 0.49480 0.51496 0.60610
3 0.20193 0.37779 0.40386 0.49476 0.51495 0.60608
4 0.20194 0.37779 0.40381 0.49478 0.51492 0.60605
5 0.20181 0.37780 0.40386 0.49469 0.51495 0.60612
6 0.20181 0.37773 0.40390 0.49463 0.51507 0.60601
7 0.20196 0.37774 0.40391 0.49466 0.51494 0.60606
8 0.20195 0.37774 0.40389 0.49462 0.51506 0.60613
9 0.20182 0.37776 0.40380 0.49474 0.51506 0.60603 
plt1 = sns.relplot(data=data2,kind="line",marker="o")
k =plt1.set(xticks=data2.index)
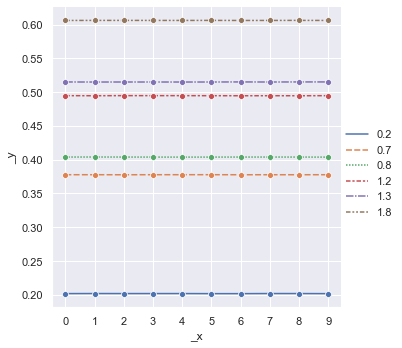
_images/FIZ228_03_LeastSquaresErrors_18_0.png 
data2.mean()

0.2    0.201900
0.7    0.377759
0.8    0.403882
1.2    0.494707
1.3    0.514983
1.8    0.606071
dtype: float64

data_stats = pd.DataFrame(data2.mean())
data_stats.rename(columns={0:'dmean'}, inplace=True )
data_stats['dvar'] = data2.var()
data_stats['dstd'] = data2.std()
data_stats
dmean dvar dstd
0.2 0.201900 4.155556e-09 0.000064
0.7 0.377759 1.076667e-09 0.000033
0.8 0.403882 2.595556e-09 0.000051
1.2 0.494707 4.467778e-09 0.000067
1.3 0.514983 3.778889e-09 0.000061
1.8 0.606071 1.698889e-09 0.000041 
data_stats.dstd # Unbiased

0.2    0.000064
0.7    0.000033
0.8    0.000051
1.2    0.000067
1.3    0.000061
1.8    0.000041
Name: dstd, dtype: float64
\[\sigma = \sqrt{\frac{\sum_{i}{\left(x_i - \bar{x}\right)^2}}{N}}\;\text{(Population)}\]

or

\[\sigma = \sqrt{\frac{\sum_{i}{\left(x_i - \bar{x}\right)^2}}{N-1}}\;\text{(Sample)}\]
import numpy as np
N = data2.shape[0]
for coll in list(data2.columns):
    s_dev = 0
    s_mean = data2.loc[:,coll].mean()
    #print(s_mean)
    for x_i in data2.loc[:,coll]:
        # print (x_i)
        s_dev += (x_i - s_mean)**2
    s_dev = np.sqrt(s_dev/(N))
    print("{:s}: {:.6f}".format(coll,s_dev))

0.2: 0.000061
0.7: 0.000031
0.8: 0.000048
1.2: 0.000063
1.3: 0.000058
1.8: 0.000039

data2.std(ddof=0) # Biased

0.2    0.000061
0.7    0.000031
0.8    0.000048
1.2    0.000063
1.3    0.000058
1.8    0.000039
dtype: float64

Average over all the sample deviations should be equal to the deviation of the population!

For more information on this Bessel’s Correction, check: http://mathcenter.oxford.emory.edu/site/math117/besselCorrection/

Types of Errors

True error (\(E_t\))

\[E_t = \text{true value} - \text{approximation}\]

Absolute error (\(\left|E_t\right|\))

\[\left|E_t\right| = \left|\text{true value} - \text{approximation}\right|\]

True fractional relative error

\[\frac{\text{true value} - \text{approximation}}{\text{true value}}\]

True percent relative error (\(\varepsilon_t\))

\[\varepsilon_t = \frac{\text{true value} - \text{approximation}}{\text{true value}}\,100\%\]

But what if we don’t know the true value?..

Approximate percent relative error (\(\varepsilon_a\))

\[\varepsilon_a = \frac{\text{present approximation} - \text{previous approximation}}{\text{present approximation}}\,100\%\]

Computations are repeated until \(\left|\varepsilon_a\right| < \left|\varepsilon_s\right|\) (\(\varepsilon_s\) is the satisfactory precision criterion).

The result is correct to at least \(n\) significant figures given that:

\[\varepsilon_s=\left(0.5\times10^{2-n}\right)\,\%\]

Example:

\[e^x = 1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\dots+\frac{x^n}{n!}+\dots\]

To estimate \(e^{0.5}\) so that the absolute value of the approximate error estimate falls below an error criterion conforming to 3 significant figures, how many terms do you need to include?

Solution:

\(\varepsilon_s=(0.5\times 10^{2-3})\,\%\)

eps_s = 0.5*10**(2-3)
print("{:.2f}%".format(eps_s))

0.05%

eps_s = 0.5*10**(2-3)

x = 0.5
eps_a = 1000
e_prev = 0
no_of_terms = 0
print("{:>3} {:^13}\t{:^10}".format("#","e","E_a"))
while(eps_a > eps_s):
    e_calculated = e_prev + x**no_of_terms/np.math.factorial(no_of_terms)
    eps_a = np.abs(((e_calculated - e_prev)/e_calculated))*100
    print("{:3d}:{:10.6f}\t{:16.5f}".format(no_of_terms+1,e_calculated,eps_a))
    e_prev = e_calculated
    no_of_terms += 1

  #       e      	   E_a    
  1:  1.000000	       100.00000
  2:  1.500000	        33.33333
  3:  1.625000	         7.69231
  4:  1.645833	         1.26582
  5:  1.648438	         0.15798
  6:  1.648698	         0.01580

eps_s = 0.5*10**(2-3)
e_sqrt_real = np.sqrt(np.e)

x = 0.5
eps_a = 1000
e_sqrt_prev = 0
no_of_terms = 0
print("{:>3} {:^13}{:^20}{:^12}".format("#","e_calc","E_a","E_t"))
while(eps_a > eps_s):
    e_sqrt_calculated = e_sqrt_prev + x**no_of_terms/np.math.factorial(no_of_terms)
    eps_a = np.abs(((e_sqrt_calculated - e_sqrt_prev)/e_sqrt_calculated))*100
    eps_t = np.abs((e_sqrt_real - e_sqrt_calculated)/e_sqrt_real)*100
    print("{:3d}:{:10.6f}{:16.5f}{:16.5f}".format(no_of_terms+1,e_sqrt_calculated,eps_a,eps_t))
    e_sqrt_prev = e_sqrt_calculated
    no_of_terms += 1

  #    e_calc            E_a             E_t     
  1:  1.000000       100.00000        39.34693
  2:  1.500000        33.33333         9.02040
  3:  1.625000         7.69231         1.43877
  4:  1.645833         1.26582         0.17516
  5:  1.648438         0.15798         0.01721
  6:  1.648698         0.01580         0.00142

How good is a mean?

Once again, consider our free fall data:

data2
0.2 0.7 0.8 1.2 1.3 1.8
0 0.20188 0.37775 0.40391 0.49475 0.51501 0.60603
1 0.20197 0.37779 0.40397 0.49464 0.51491 0.60610
2 0.20193 0.37770 0.40391 0.49480 0.51496 0.60610
3 0.20193 0.37779 0.40386 0.49476 0.51495 0.60608
4 0.20194 0.37779 0.40381 0.49478 0.51492 0.60605
5 0.20181 0.37780 0.40386 0.49469 0.51495 0.60612
6 0.20181 0.37773 0.40390 0.49463 0.51507 0.60601
7 0.20196 0.37774 0.40391 0.49466 0.51494 0.60606
8 0.20195 0.37774 0.40389 0.49462 0.51506 0.60613
9 0.20182 0.37776 0.40380 0.49474 0.51506 0.60603 
data_stats
dmean dvar dstd
0.2 0.201900 4.155556e-09 0.000064
0.7 0.377759 1.076667e-09 0.000033
0.8 0.403882 2.595556e-09 0.000051
1.2 0.494707 4.467778e-09 0.000067
1.3 0.514983 3.778889e-09 0.000061
1.8 0.606071 1.698889e-09 0.000041

scipy.optimize.minimize to the rescue!

data2['0.2'].shape

(10,)

from scipy.optimize import minimize

def fun_err(m,x):
    err = 0
    for x_i in x:
        err += (x_i - m)**2
    err = np.sqrt(err/x.shape[0])
    return err

fun_err(data2['0.2'].mean(),data2['0.2'])

6.11555394056866e-05

fun_err(data2['0.2'].mean()+1,data2['0.2'])

1.00000000187

minimize(fun_err,data2['0.2'].mean(),args=(data2['0.2']),tol=1E-3)

      fun: 6.11555394056866e-05
 hess_inv: array([[1]])
      jac: array([0.00012183])
  message: 'Optimization terminated successfully.'
     nfev: 2
      nit: 0
     njev: 1
   status: 0
  success: True
        x: array([0.2019])

data2['0.2'].mean()

0.20190000000000002

list(data2.columns)

['0.2', '0.7', '0.8', '1.2', '1.3', '1.8']

data_stats.loc['0.2','dmean']

0.20190000000000002

print("{:^5}: {:^8} ({:^8})".format("col","min","mean"))
for col in list(data2.columns):
    res_min = minimize(fun_err,1,args=(data2[col]))
    print("{:^5}: {:8.6f} ({:8.6f})".format(col,float(res_min.x),data_stats.loc[col,'dmean']))

 col :   min    (  mean  )
 0.2 : 0.201900 (0.201900)
 0.7 : 0.377759 (0.377759)
 0.8 : 0.403882 (0.403882)
 1.2 : 0.494707 (0.494707)
 1.3 : 0.514983 (0.514983)
 1.8 : 0.606071 (0.606071)

Couldn’t the cost function be better?

def fun_err2(m,x):
    err = 0
    for x_i in x:
        err += (x_i - m)**2
    #err = np.sqrt(err/x.shape[0])
    return err

fun_err2(data2['0.2'].mean(),data2['0.2'])

3.740000000000487e-08

minimize(fun_err2,data2['0.2'].mean(),args=(data2['0.2']))

      fun: 3.740000000000487e-08
 hess_inv: array([[1]])
      jac: array([1.49011612e-07])
  message: 'Optimization terminated successfully.'
     nfev: 2
      nit: 0
     njev: 1
   status: 0
  success: True
        x: array([0.2019])

print("{:^5}: {:^8} ({:^8})".format("col","min","mean"))
for col in list(data2.columns):
    res_min = minimize(fun_err2,1,args=(data2[col]))
    print("{:^5}: {:8.6f} ({:8.6f})".format(col,float(res_min.x),data_stats.loc[col,'dmean']))

 col :   min    (  mean  )
 0.2 : 0.201900 (0.201900)
 0.7 : 0.377759 (0.377759)
 0.8 : 0.403882 (0.403882)
 1.2 : 0.494707 (0.494707)
 1.3 : 0.514983 (0.514983)
 1.8 : 0.606071 (0.606071)

def fun_err3(m,x):
    err = 0
    for x_i in x:
        err += np.abs(x_i - m)
    #err = np.sqrt(err/x.shape[0])
    return err

fun_err3(data2['0.2'].mean(),data2['0.2'])

0.0005599999999999772

minimize(fun_err3,data2['0.2'].mean(),args=(data2['0.2']))

      fun: 0.0005000017699288428
 hess_inv: array([[7.97330502e-06]])
      jac: array([1.76244418])
  message: 'Desired error not necessarily achieved due to precision loss.'
     nfev: 120
      nit: 1
     njev: 54
   status: 2
  success: False
        x: array([0.20193])

data_exp = pd.DataFrame(data_stats.dmean)

data_exp
dmean
0.2 0.201900
0.7 0.377759
0.8 0.403882
1.2 0.494707
1.3 0.514983
1.8 0.606071 
def freefall_err(g,y_exp,t):
    err = 0
    y_theo = 0.5*g*t**2
    err = (y_theo - y_exp)**2
    return np.sum(err)

y_exp = np.array(list(data_exp.index))
print(y_exp)

['0.2' '0.7' '0.8' '1.2' '1.3' '1.8']

y_exp.dtype

dtype('<U3')

y_exp = np.array(list(data_exp.index),dtype=float)
y_exp.dtype

dtype('float64')

print(y_exp)

[0.2 0.7 0.8 1.2 1.3 1.8]

t = np.array(list(data_exp.dmean[:]))
print(t)

[0.2019   0.377759 0.403882 0.494707 0.514983 0.606071]

We can do that manually!… (???)

freefall_err(9,y_exp,t)

0.05069082651399326

freefall_err(9.1,y_exp,t)

0.0388634097682171

for g in np.arange(9,10,0.1):
    print("{:5.3f}:{:10.6f}".format(g,freefall_err(g,y_exp,t)))

9.000:  0.050691
9.100:  0.038863
9.200:  0.028605
9.300:  0.019915
9.400:  0.012795
9.500:  0.007243
9.600:  0.003261
9.700:  0.000847
9.800:  0.000002
9.900:  0.000726

for g in np.arange(9.7,9.9,0.01):
    print("{:5.3f}:{:10.6f}".format(g,freefall_err(g,y_exp,t)))

9.700:  0.000847
9.710:  0.000692
9.720:  0.000552
9.730:  0.000429
9.740:  0.000321
9.750:  0.000228
9.760:  0.000152
9.770:  0.000091
9.780:  0.000045
9.790:  0.000016
9.800:  0.000002
9.810:  0.000004
9.820:  0.000021
9.830:  0.000055
9.840:  0.000103
9.850:  0.000168
9.860:  0.000248
9.870:  0.000344
9.880:  0.000456
9.890:  0.000583
9.900:  0.000726

for g in np.arange(9.79,9.81,0.001):
    print("{:5.3f}:{:10.8f}".format(g,freefall_err(g,y_exp,t)))

9.790:0.00001591
9.791:0.00001382
9.792:0.00001188
9.793:0.00001010
9.794:0.00000848
9.795:0.00000701
9.796:0.00000570
9.797:0.00000455
9.798:0.00000355
9.799:0.00000272
9.800:0.00000203
9.801:0.00000151
9.802:0.00000114
9.803:0.00000093
9.804:0.00000088
9.805:0.00000098
9.806:0.00000124
9.807:0.00000166
9.808:0.00000223
9.809:0.00000296
9.810:0.00000385

res_min = minimize(freefall_err,x0=1,args=(y_exp,t))
print(res_min)

      fun: 8.748023164225757e-07
 hess_inv: array([[6.3736979]])
      jac: array([-2.0061961e-09])
  message: 'Optimization terminated successfully.'
     nfev: 10
      nit: 4
     njev: 5
   status: 0
  success: True
        x: array([9.8038438])

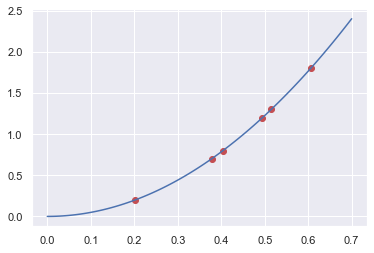
import matplotlib.pyplot as plt
plt.plot(t,y_exp,"or")
tt = np.linspace(0,0.7,100)
plt.plot(tt,0.5*res_min.x*tt**2,"-b")
plt.show()
_images/FIZ228_03_LeastSquaresErrors_68_0.png

Least Squares (numpy.linalg.lstsq & scipy.linalg.lstsq & scipy.optimize.least_squares) but not least! 8)

NumPy and SciPy’s linalg.lstsq functions works similar to each other, solving the matrix equation \(Ax=b\) but as the coefficients matrix \(A\) must be defined as a matrix, we add a “zeros” column next to \(\tfrac{1}{2}t^2\) values, to indicate that our equation is of the form:

\[\left(\frac{1}{2}t^2\right)g^1 + (0)g^0 = y_{exp}\]
A = np.vstack([(0.5*t**2),np.zeros(len(t))]).T
A

array([[0.02038181, 0.        ],
       [0.07135093, 0.        ],
       [0.08156033, 0.        ],
       [0.12236751, 0.        ],
       [0.13260375, 0.        ],
       [0.18366103, 0.        ]])

numpy.linalg.lstsq

g_ls_np, _ = np.linalg.lstsq(A,y_exp,rcond=None)[0]
g_ls_np

9.803843815755029

scipy.linalg.lstsq

import scipy as sp
g_ls_sp, _ = sp.linalg.lstsq(A,y_exp)[0]
g_ls_np

9.803843815755029

scipy.optimize.least_squares

SciPy’s optimize.least_squares is a totally different beast, though. It tries to minimize the cost function (e.g., errors). Its main difference from the above two is that it supports nonlinear least-squares problems and also accepts boundaries on the variables. It is included here only to give you an idea (as it is more or less the same with the optimize.minimize ;)

def fun_err_g(g):
    return (0.5*g*t**2 - y_exp)**2

g_ls_sp_opt = sp.optimize.least_squares(fun_err_g,10).x[0]
g_ls_sp_opt

9.81433312096714

Various Definitions

Sum of the squares of the data residuals (\(S_t\))

\[S_t = \sum_{i}{\left(y_i - \bar{y}\right)^2}\]

(\(\leftrightarrow\) Standard deviation \(\sigma=\sqrt{\frac{S_t}{n-1}}\), variance \(\sigma^2=\frac{\sum_{i}{\left(y_i-\bar{y}\right)^2}}{n-1}=\frac{\sum_{i}{y_i^2}-\left(\sum_{i}{y_i}\right)^2/n}{n-1}\))

Coefficient of variation

\[\text{c.v.} = \frac{s_y}{\bar{y}}\times\,100\%\]

Sum of the squares of the estimate residuals (\(S_r\))

\[S_r = \sum_{i}{e_i^2}=\sum_{i}\left(y_i-a_0-a_1 x_i\right)^2\]

Standard error of the estimate: (\(s_{y/x}\))

\[s_{y/x}= \sqrt{\frac{S_r}{n-2}}\]

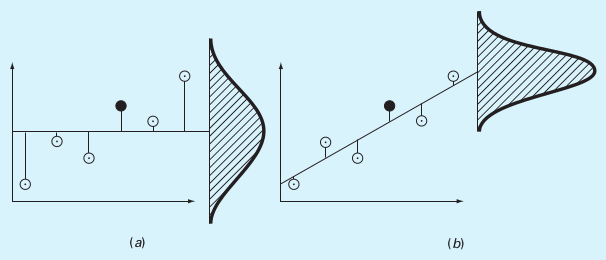standard_errors.png (a) \(S_t\), (b) \(S_r\)

(Source: S.C. Chapra, Applied Numerical Methods with MATLAB)

Coefficient of Determination (\(r^2\))

\[r^2 = \frac{S_t-S_r}{S_t}\]

References

previous

Visualization of datasets

next

Regression